Численный и приближенный анализ
-
С помощью приближенной формулы
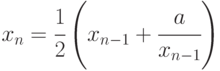
-
для нахождения квадратного корня из числа а, вычислить приближенные значения корня из 2 с точностью 0,01 и 0,001. Сравните объем вычислительной работы. Докажите, что для всякого a>0 найдется N, что xN достаточно (с любой точностью) близко к
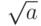 , т.е. корень из положительного числа можно вычислить с какой угодно точностью по рекуррентной формуле для xn
. Указание: положить
, т.е. корень из положительного числа можно вычислить с какой угодно точностью по рекуррентной формуле для xn
. Указание: положить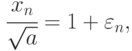
разделить выражение для xn на
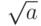 и учесть это равенство; из полученного равенства
и учесть это равенство; из полученного равенства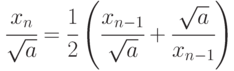
следует, что
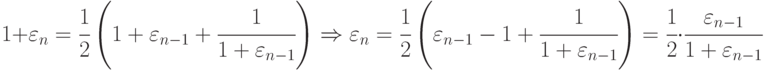
-
Решить аналитически, графически и приближенно (методом бисекций, с точностью не менее 0,01 ) уравнение x3–x2–5х+6=0. Сравнить вычислительные затраты (время) и точность найденных корней. Указание: для аналитического решения уравнение записать в виде
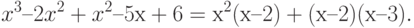
- Даны значения числа зарегистрированных безработных в РФ (млн. чел.) за пять лет, начиная с 1992 года: 3,584 ; 4,160 ; 5,478 ; 6,040 ; 6,800. Построить интерполянту по этим данным и найти численность безработных в 1993 году. Осуществить прогноз на 1997 и 1999 год. Сравнить с реальными данными. Оценить точность прогноза. Указание: точность прогноза оценить в относительных ошибках.
- По данным предыдущей задачи найти численно производную заданной дискретной функции числа безработных (темп роста безработных). Указание: продифференцируйте найденную выше интерполянту и вычислите значение производной.
- Если данные получены в результате измерения объекта или системы, находящейся в развитии без лимитирующих факторов, то есть прямой смысл искать соответствующую эмпирическую формулу вида y=Aeax . Обоснуйте это утверждение. Указание: отсутствие лимитирования ведет к экспоненциальному росту, согласно уравнению показательного роста.
-
В качестве эмпирических функций в социально-гуманитарных и эколого-экономических областях часто используются зависимости:
- степенная –
 ,
, - показательная –
 ,
, - экспоненциальная –
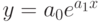 ,
, - логистическая –
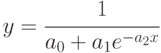 .
.
Выбор функции в каждом конкретном случае осуществляют на основании ряда свойств. Часто о виде модели можно судить по соотношениям (и по скорости изменения значений функции) – по приращениям:
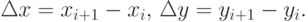
Какие функции лучше подбирать в случаях:
-
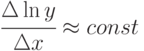 ;
; -
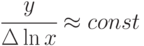 ;
; -
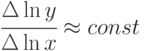 .
.
Обоснуйте ответ. Указание: если отношение малых приращений функции и аргумента постоянно, то производная, соответствующая этим приращениям близка к постоянной.
- степенная –
-
Подобрать эмпирическую формулу
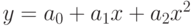 при равноточных данных, если зависимость транспортных издержек в руб. (величина y ) при перевозке единицы груза на х км выражена нижеследующей таблицей:
при равноточных данных, если зависимость транспортных издержек в руб. (величина y ) при перевозке единицы груза на х км выражена нижеследующей таблицей:Определить стоимость перевозки (транспортных издержек) при необходимости перевозки груза на расстояние:
- 1,9 км;
- 2,5 км;
- 3,5 км.
Указание: используя метод наименьших квадратов и систему нормальных уравнений определить неизвестные три коэффициента искомой зависимости.
- Необходимо решить приближенно систему трех уравнений с тремя неизвестными, если коэффициенты aij
( i,j=1,2,3 ) системы равны интегралам от функции
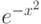 в границах от 0 до i+j, а свободные члены bi=i. Указание: вычислить сначала приближенно интегралы (экономно!), например, по формуле трапеций.
в границах от 0 до i+j, а свободные члены bi=i. Указание: вычислить сначала приближенно интегралы (экономно!), например, по формуле трапеций. - Торговая фирма закупила товар. Необходимо развести этот товар в два магазина фирмы: в первый магазин необходимо доставить не менее 40 комплектов, а во второй – не менее 20 комплектов. Доставка одного комплекта в первый магазин обходиться в 100 руб., а во второй магазин – 300 руб. Прибыль от реализации одного комплекта товара первого вида равна 500 руб., а второго товара – 700 руб. Необходимо составить такой график перевозки, чтобы чистый доход (прибыль от реализации минус стоимость доставки) была бы максимальной. Сформулировать как задачу математического программирования и решить. Указание: записать в виде транспортной задачи; функция цели – чистый доход (прибыль от реализации минус стоимость доставки).
- Пенсионному фонду требуется составить оптимальный график выплаты пенсий трех видов в сумме 100, 200, 300 тыс. руб. План выплаты должен предусматривать наименьший срок выплат. Первый вид пенсий должен быть выплачен в течение не менее 8 дней, второй – в течение не менее 12 дней, третий вид – в течение 9 дней. Составить план выплат с наименьшим общим сроком выплат, если пенсионный фонд может в день выплачивать не более 50, 70, 100 тыс. руб. пенсии каждого вида. Сформулировать эту содержательно изложенную задачу как задачу математического программирования и решить. Указание: записать как задачу линейного программирования ; функция цели – срок выплаты.
