Опубликован: 22.01.2008 | Доступ: свободный | Студентов: 3499 / 685 | Оценка: 4.05 / 4.28 | Длительность: 03:50:00
Тема: Математика
Специальности: Математик
Практическая работа 3:
Координаты и векторы
< Практическая работа 2 || Практическая работа 3 || Самостоятельная работа 1 >
Аннотация: Решение типовых задач в базовых системах координат (декартова прямоугольная, полярная) с векторными операциями на плоскости, в пространстве, обучение реферированию и Интернет–поиску по этой теме
Ключевые слова: проекция, система координат, коллинеарность, компланарность, разложение вектора, скалярная величина, векторная величина
Задачи
- Постройте вектор длины 5 единиц и направления, совпадающего с направлением возрастания чисел числовой прямой. Постройте противоположный ему вектор. Указание: направление первого вектора – луч x >= 0 ; второго – луч x <= 0.
- Постройте вектор длины 6 единиц и направления, совпадающего с направлением убывания чисел числовой прямой. Постройте противоположный ему вектор. Указание: направление первого вектора – луч x <= 0.
- Постройте вектор длины 7 единиц и направления, совпадающего с направлением биссектрисы первого координатного угла. Постройте противоположный ему вектор. Указание: направление первого вектора – луч y = x, x >= 0.
- Постройте проекции векторов задач 1-3 на оси координат. Найдите вектор суммы этих проекций. Указание: изобразите все три вектора на одном чертеже и используйте правило построения суммы векторов.
- Постройте и запишите вектора в полярной системе координат для всех задач 1-3. Указание: использовать формулы перехода от декартовой системы координат к полярной.
- Выпишите по полярным координатам
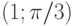 декартовы координаты вектора. Указание: использовать формулы перехода от полярных координат декартовы координаты.
декартовы координаты вектора. Указание: использовать формулы перехода от полярных координат декартовы координаты. - Постройте два коллинеарных вектора в пространстве. Запишите их координаты и проверьте выполнение условия коллинеарности. Указание: коллинеарные векторы лежат на параллельных или совпадающих прямых.
- Постройте два компланарных вектора в пространстве. Запишите их координаты и проверьте выполнение условия компланарности. Указание: компланарные векторы лежат в одной плоскости.
- Выяснить, какие вектора равны между собой, если эти вектора заданы следующими координатами: (1,1,0), (0,1,1), (1,1,1), (1,0), (sin90, cos90, cos90). Указание: равенство векторов возможно лишь тогда, когда равны все соответствующие координаты.
- Постройте вектор по его проекциям на оси координат x, y, z, соответственно, (1,1), (2.0), (1,3). Указание: использовать разложение вектора по его проекциям.
Темы научных исследований и рефератов (Интернет-листов)
- История и предпосылки появления и использования систем координат и их эволюция. Примеры.
- Виды и применения различных систем координат с древнейших времен и до наших дней. Примеры.
- Скалярные и векторные величины. Общее и различное. Взаимосвязи и взаимообусловленность. Примеры.
- Теоремы школьной планиметрии и их векторное изложение.
- Теоремы школьной стереометрии и их векторное изложение.
- Проекции в природе, науке, технике.
- Ортонормированные системы векторов и их использование.
- Разложения векторов по системам других векторов. Линейная независимость и зависимость векторов.
- Гуманитарные приложения векторов. Примеры.
- Социально-экономические приложения векторов. Примеры.
< Практическая работа 2 || Практическая работа 3 || Самостоятельная работа 1 >
