Введение в математику. Практикум
[+]
Опубликован: 22.01.2008 | Доступ: свободный | Студентов: 3451 / 676 | Оценка: 4.05 / 4.28 | Длительность: 03:50:00
Тема: Математика
Специальности: Математик
Теги: алгебра, анализ, вычисления, гипербола, графика, дифференциал, евклидово пространство, жизненный цикл продукта, игры, интернет-поиск, исследование операций, исследования, история, комбинаторика, минимакс, мутация, образование, приложения, программирование, процедуры, расходимость ряда, статистика, точность прогноза, характеристическое уравнение
Практическая работа 9:

Интегрирование
A
|
версия для печати
< Практическая работа 8 || Практическая работа 9 || Самостоятельная работа 3 >
Аннотация: Решение типовых задач интегрального исчисления, обучение реферированию и Интернет–поиску по этой теме
Ключевые слова: первообразная, интеграл, метод замены переменной, интегрирование, интегрирование по частям, парабола, Гипербола, дифференциал

Задачи

  1. Исходя из определения первообразной найти первообразную для функции вида:

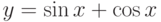    • y=\sin x+\cos x ;
    • y=\sqrt{x} ;
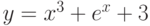    • y=x^3+e^x+3.

    Указание: использовать свойство первообразной (F'(x)=f(x)).

  2. Найти первообразную функции по формулам:

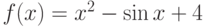    • f(x)=x^2-\sin x + 4 ;
    • f(x)=(2x-7)^3 ;
    • f(x)=\sqrt[3]{x} – 3e^x .

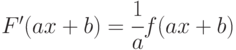    Указание: а), б) – табличные функции; в) – использовать формулу первообразной от линейного аргумента – F'(ax+b)=\cfrac{1}{a}f(ax+b) .

  3. Найти первообразную функции, предварительно упростив функцию: 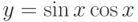y=\sin x \cos x. Указание: использовать формулу синуса двойного угла.

  4. Вычислить неопределенный интеграл от функции

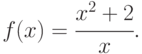
    f(x)=\cfrac{x^2+2}{x}.

    График какой функции из этого семейства первообразных проходит через точку А(1;1)? Указание: произвести предварительно почленное деление.

  5. Вычислить определенный интеграл от функции
    f(x)=\cfrac{x^2+2}{x}
    на отрезке [2;3]. Указание: произвести предварительно почленное деление.
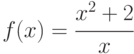
  6. Вычислить определенный интеграл от функции 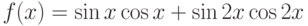f(x)=\sin x \cos x + \sin{2x} \cos{2x} на отрезке [0;\pi ]. Указание: использовать соответствующие школьные тригонометрические формулы.

  7. Вычислить интеграл методом замены переменной интегрирования:

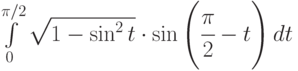    • \int\limits_0^{\pi / 2}{\sqrt{1-\sin^2t}\cdot\sin{\left(\cfrac{\pi}{2}-t\right)}}\,dt ;
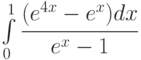    • \int\limits_0^1{\cfrac{(e^{4x}-e^x)dx}{e^x-1}} ;
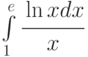    • \int\limits_1^e{\cfrac{\ln x dx}{x}}.

    Указание: заменить – а) sint = y ; б) ex=y ; в) ln(x)=y.

  8. Вычислить интеграл по частям:

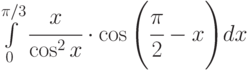    • \int\limits_0^{\pi/3}{\cfrac{x}{\cos^2 x}\cdot\cos{\left(\cfrac{\pi}{2}-x\right)}dx} ;
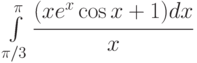    • \int\limits_{\pi/3}^{\pi}{\cfrac{(xe^x \cos{x}+1)dx}{x}} ;
    • \int\limits_1^3{\cfrac{dx}{\sin^2{\pi x}\cos^2{\pi x}}}.

    Указание: предварительно применить – а) формулу приведения; б) почленное деление, а затем двукратное интегрирование по частям ; в) формулу синуса двойного аргумента.

  9. Вычислить площадь фигуры ограниченной следующими линиями: y=(x—1)2 , x2—0,5y2=1. Указание: нарисовать эти параболу и гиперболу.
  10. Вычислить площадь фигуры ограниченной следующими линиями: y=sinx, y=cosx, x=0. Указание: нарисовать графики линий (эскизы).

Темы научных исследований и рефератов (Интернет-листов)

  1. Первообразная, ее происхождение.
  2. Исторические предпосылки формирования интегрального исчисления.
  3. Интегральное исчисление и его эволюция.
  4. Приложения интегрирования в социально-экономических областях.
  5. Приложения интегрирования в гуманитарных областях.
  6. Интегрирование функции многих переменных.
  7. Несобственные интегралы.
  8. Методы интегрирования.
  9. Фундаментальность интегрального исчисления как метода исследования законов природы и общества.
  10. Дифференциал и интеграл – единство и борьба противоположностей.
Дальше >>
< Практическая работа 8 || Практическая работа 9 || Самостоятельная работа 3 >

Вопросы и ответы

вопросов: 3
Антон Бабарыкин
Антон Бабарыкин
ответить
Татьяна Бурунова
Татьяна Бурунова
ответить