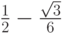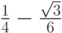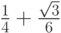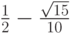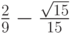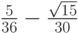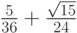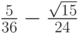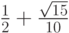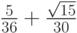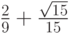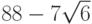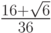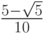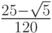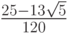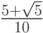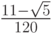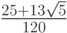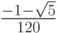Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений
9.4. Численные методы решения ЖС ОДУ. Семейства неявных методов Рунге - Кутты и Розенброка
Рассмотрим другие методы для численного решения как линейных жестких систем ОДУ вида (9.1), так и нелинейных систем общего вида
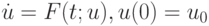
и автономных ЖС ОДУ
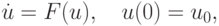
см. также [9.1], [9.4], [9.9], [9.13], [9.14], [9.15], [9.16]. Из соображений устойчивости метода предпочтение естественно отдать неявным методам. Простейшими из них являются:
-
неявный метод Эйлера (приведем его вид для случая автономной ЖС ОДУ, для неавтономной системы формулы очевидны):
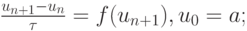
-
метод трапеций
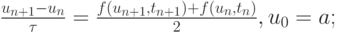
-
метод прямоугольников (правило средней точки)
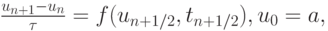
где
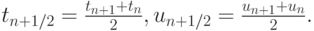
Среди одношаговых методов для решения жестких систем наиболее известны методы Рунге-Кутты. Все приведенные в данном параграфе формулы можно рассматривать как частные случаи неявных одно - и двухстадийных методов из этого семейства. Не останавливаясь на получении приводимых коэффициентов, выпишем наиболее известные из формул Рунге - Кутты, используя таблицу Бутчера. О представлении методов Рунге - Кутты в виде таблиц Бутчера — в "Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений" .
Отметим, что в отличие от рассматриваемых выше явных методов, при использовании неявных схем Рунге - Кутты матрица коэффициентов метода в таблице Бутчера — заполненная, и для определения вспомогательных векторов, входящих в функцию приращения, приходится решать систему нелинейных алгебраических уравнений.
- Методы Гаусса соответственно 2 - го, 4 - го, и 6 - го порядков представлены в табл. 9.1, 9.2, 9.3. Основаны эти методы на соответствующих квадратурных формулах Гаусса, рассмотренных в "Численное интегрирование" . Первый метод совпадает с правилом средней точки. Второй метод (4 - го порядка) носит название метода Хаммера - Холлинсворта.
- Методы Радо IIA порядков 1, 3, 5 представлены соответственно в табл. 9.4, 9.5, 9.6. Основаны на квадратурных формулах Радо, принадлежащих к семейству формул Гаусса. Метод первого порядка является неявным методом Эйлера.
- Методы Лобатто IIIА 2-го, 4-го и 6-го порядков точности см. в
табл. 9.7, 9.8, 9.9 и 9.10
соответственно. Видно, что метод второго порядка точности является неявным методом трапеций.
Рассмотрим теперь, как строится функция устойчивости для методов Рунге - Кутты [9.4]. Уже отмечалось выше, что при построении функции устойчивости рассматривается модельное уравнение вида
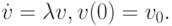
Запишем теперь метод Рунге - Кутты для решения приведенного выше уравнения в общей форме с использованием новых переменных Y:

Приведенные выше формулы можно рассматривать как систему линейных уравнений относительно новых переменных Y1, ..., Yk, vn + 1 следующего вида:
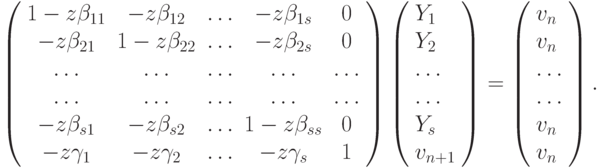
Необходимо выразить vn + 1 через vn. Для этого воспользуемся правилом Крамера. Ответ можно записать в следующей форме:
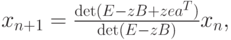
где E — единичная матрица размера S x S, B - матрица коэффициентов
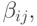 входящая в таблицу Бутчера, E — единичный вектор размерности S (столбец), aT — строка коэффициентов
входящая в таблицу Бутчера, E — единичный вектор размерности S (столбец), aT — строка коэффициентов  входящая в таблицу Бутчера, S — число стадий метода Рунге - Кутты.
входящая в таблицу Бутчера, S — число стадий метода Рунге - Кутты.Условием устойчивости метода будет

Одноитерационные методы Розенброка. Розенброком был предложен класс неявных методов, в котором не решается система нелинейных уравнений. В простейшем случае для автономной системы уравнений методы типа Розенброка могут иметь вид [9.3]
![$ (E - a {\tau}B - b {\tau}^2 B^2 ) \frac{u_{n + 1} - u_n}{{\tau}} =
f[u_n + c{\tau}f(u_n)] . $](/sites/default/files/tex_cache/60d15cfbafa30ed5dafc0ab36cc40b5c.png)
Здесь
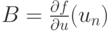
Например, для схемы третьего порядка точности получим
a = 1, 077; b = - 0, 372; c = - 0, 577 .
Такую схему иногда называют методом с одной итерацией, имея в виду, что вычисление обратной матрицы сравнимо по количеству арифметических операций с одной итерацией метода Ньютона. Преимущество методов типа Розенброка перед прочими классами численных методов ЖС ОДУ заключается в том, что для определения решения на верхнем временном слое необходимо решать уже линейную систему алгебраических уравнений.
Рассмотрим связь между методами Розенброка и Рунге - Кутты.
Определение. ([9.9]) S - стадийный метод Розенброка для решения автономной системы ЖС ОДУ имеет вид
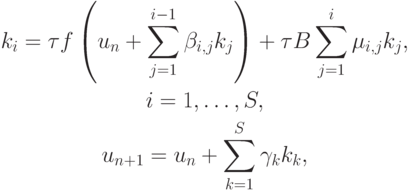
где 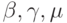 — управляющие коэффициенты метода.
Как и выше, матрица Якоби правой части системы B вычисляется по
данным в точке tn. Связь последних формул с выражениями для явных методов Рунге - Кутты очевидна.
— управляющие коэффициенты метода.
Как и выше, матрица Якоби правой части системы B вычисляется по
данным в точке tn. Связь последних формул с выражениями для явных методов Рунге - Кутты очевидна.
Несколько сложнее представляются методы Розенброка в случае неавтономной ЖС ОДУ [9.9]:
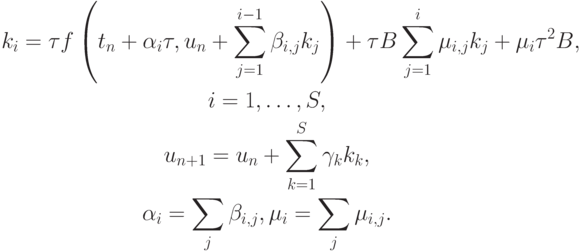
Вывод условий порядка методов Розенброка — достаточно громоздкий, и всем заинтересованным читателям можно рекомендовать разобраться в выкладках в книге [9.9]. Отметим, что широкое распространение получают в последнее время вложенные методы Розенброка высокого порядка аппроксимации, имеющие очень хорошие вычислительные качества. Возможно, что новые методы типа Розенброка способны будут вытеснить из вычислительной практики наиболее распространенные до этого в вычислительной практике методы Гира.