Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений
9.3. Решение линейных ЖС ОДУ и вычисление матричной экспоненты
Рассмотрим один из наиболее простых численных методов решения жестких линейных систем ОДУ [9.10], основанный на представлении решения в явном виде
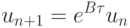
для линейных систем жестких ОДУ вида
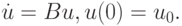
Его численная реализация связана с вычислением матричной экспоненты. О свойствах матричной экспоненты (и в целом функций от матриц) можно прочитать в [9.11]. Использование для этого разложения в ряд Тейлора
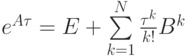
представляется непригодным, так как простые оценки показывают, что по
вычислительным затратам этот алгоритм сопоставим с методом Эйлера с шагом  :
:
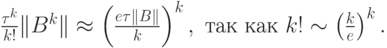
Следовательно, для того, чтобы k - й член разложения ряда Тейлора был, по крайней мере, порядка O(1), необходимо выполнение условия

что соответствует условию численного интегрирования с шагом  Количество членов ряда при этом
Количество членов ряда при этом 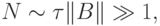 что неприемлемо для решения.
что неприемлемо для решения.
Представим экспоненту в следующем эквивалентном виде:
![$ e^{{B}{\tau}} = (e^{{\tau}A/2^p})^{2^p} \approx {\left[{E + \frac{{\tau}}{2^p}B + \ldots + \frac{1}{k!}{\left({\frac{{\tau}}{2^p}}\right)}^k B^k}\right]}^{2^p}.$](/sites/default/files/tex_cache/3ee1933b5bd77d67ad13acf21a22a1dc.png)
При этом значение параметра p выбирают таким, чтобы

и можно было использовать ряд Тейлора с небольшим количеством членов. Действительно, в этом случае
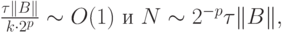
что вполне приемлемо при соответствующем выборе параметра p.
В этом алгоритме сначала вычисляют матрицу
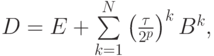
затем  путем последовательных перемножений. При таком способе вычисления матрицы также имеется опасность, связанная с тем, что при некоторых p,
путем последовательных перемножений. При таком способе вычисления матрицы также имеется опасность, связанная с тем, что при некоторых p,  слагаемые, соответствующие мягкой части спектра, окажутся много меньше единицы (и слагаемых, соответствующих жесткой части). В этом случае предпочтение отдается представлению
слагаемые, соответствующие мягкой части спектра, окажутся много меньше единицы (и слагаемых, соответствующих жесткой части). В этом случае предпочтение отдается представлению
![$ e^{A{\tau}} = \left[{\exp \left({- \frac{{\tau}}{2^p}{B}}\right)^{- 1}}\right]^{2^{p}}, $](/sites/default/files/tex_cache/25cfb320a3d29ca22e3918f76609fb0b.png)
а последовательность вычислений имеет вид

При этом на мягкой части спектра, поскольку 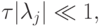 имеем
имеем
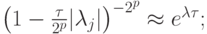
на жесткой части, поскольку теперь p небольшие и 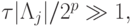 получим оценку
получим оценку
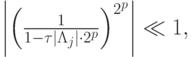
что уже приемлемо для вычислений.
