Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений
- Пограничный слой A'A. На этом участке за малое время
 траектория из точки {u0, v0} переходит в
траектория из точки {u0, v0} переходит в  - окрестность кривой f = 0. Здесь траектория почти горизонтальна и приближенно определяется дифференциальным уравнением
- окрестность кривой f = 0. Здесь траектория почти горизонтальна и приближенно определяется дифференциальным уравнением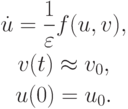
(
 так как
так как 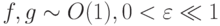 ).
).В окрестности кривой f(u, v) = 0 имеем f'u < 0, поэтому допустима оценка
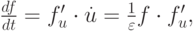
откуда видно, что f(u, v0) стремится к нулю как экспонента с показателем
т.е. f становится малой величиной (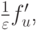
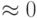 ) за время
) за время 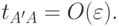
- Квазистационарный режим. Движение точки {u(t), v(t)}
продолжается уже по участку кривой AB, f(u, v) = 0
и описывается системой
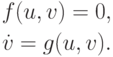
На этом участке за время
 что видно из
второго уравнения, точка подвигается от A к B, пока система ОДУ устойчива. В случае невозмущенной системы точка могла бы и далее продвигаться по участку BD, но для полной системы эта ветвь
оказывается неустойчивой (f'u > 0) и траектория
"срывается" на устойчивую ветвь CD в точке B, в которой f'u = 0.
что видно из
второго уравнения, точка подвигается от A к B, пока система ОДУ устойчива. В случае невозмущенной системы точка могла бы и далее продвигаться по участку BD, но для полной системы эта ветвь
оказывается неустойчивой (f'u > 0) и траектория
"срывается" на устойчивую ветвь CD в точке B, в которой f'u = 0. - Пограничный слой. На участке BC точка {u(t), v(t)}
"перескакивает" из B в C за малое время
 ; движение здесь, как и на ветви AB, приближенно описывается уравнениями
; движение здесь, как и на ветви AB, приближенно описывается уравнениями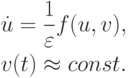
- Квазистационарный режим. Движение по ветви CD, как и по ветви AB, описывается уравнениями
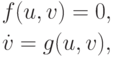
и длится
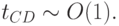
- Пограничный слой. На неустойчивой ветви DA также, как и на
ветви BC, происходит скачок из точки D за время
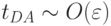 в устойчивую точку A, и т.д.
в устойчивую точку A, и т.д.Такое поведение траектории (замкнутая кривая) называется предельным циклом. Для жестких систем периодические решения называют иногда релаксационными колебаниями [9.6], [9.7].
Таким образом, это характерно для жестких систем, траектория состоит из чередующихся участков быстрого (за время
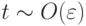 ) и медленного (за время
) и медленного (за время 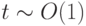 ) изменения решения.
) изменения решения.
Рассмотрим проблемы, которые могут возникнуть при численном интегрировании подобных жестких систем ОДУ. Численное интегрирование в зоне пограничного слоя, если оно необходимо исследователю, проблемы не составляет. Требуется лишь выполнение условия
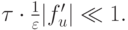
В зоне квазистационарного режима часто оказывается, что интегрирование с
таким шагом слишком дорого. Можно, правда, разрешить уравнение f(u, v) =
0 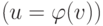 относительно u и далее
интегрировать его, предварительно реализовав алгоритм перехода на другой шаг:
относительно u и далее
интегрировать его, предварительно реализовав алгоритм перехода на другой шаг:
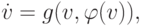
однако в случаях более сложных, построение подобных численных методов может оказаться отдельной сложной задачей.
Чаще всего в практике численных расчетов целесообразно использовать неявные схемы. В случае ЖС ОДУ неявные схемы предпочтительнее из соображений устойчивости. Так, рассматриваемую задачу можно аппроксимировать системой дискретных уравнений:
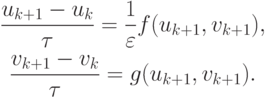
Эта система нелинейных уравнений может быть решена численно, например,
методом Ньютона. Иногда полагают, что неявные схемы позволяют проводить численное интегрирование сквозным методом с большим шагом 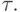 Рассмотрим, к чему это может привести.
Рассмотрим, к чему это может привести.
Первый пограничный слой будет пройден за один шаг:
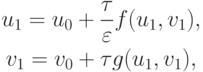
так как 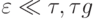 мало.
мало.
Далее следует процесс численного интегрирования на устойчивой ветви AB. В окрестности точки B поведение численного решения по неявной схеме осложняется. Это связано с тем, что рассматриваемая система в данной окрестности может иметь более одного решения. При этом, по крайней мере, одно из решений нелинейной алгебраической системы может лежать на неустойчивой ветви CD кривой f(u, v) = 0. Возможно, что при выборе большего шага интегрирования получится именно это нефизическое решение, к которому сойдутся итерации.
Такую опасность необходимо всегда учитывать при проведении численного интегрирования по неявным схемам с большим шагом.
