НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 8: Численное интегрирование

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3914 / 1195 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

7.7. Задачи

Получить локальную и глобальную оценки погрешности для формулы трапеций.
Решение. Локальную оценку погрешности получим, используя формулы для истинного члена интерполяционного полинома:

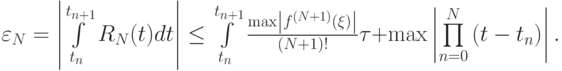
$\varepsilon_N = \left|{\int\limits_{t_n}^{t_{n + 1}}{R_N (t)dt}}\right| \le \int\limits_{t_n}^{t_{n + 1}}{\frac{{\max \left|{f^{(N + 1)} (\xi )}\right|}}{{(N + 1)!}}} {\tau}+ \max \left|{\prod\limits_{n = 0}^{N}{(t - t_n)}}\right|.$

В случае формулы трапеции имеем

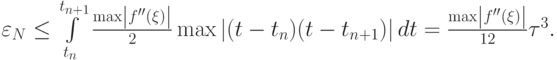
$\varepsilon_N \le \int\limits_{t_n}^{t_{n + 1}}{\frac{{\max \left|{f^{\prime\prime}(\xi )}\right|}}{2}\max \left|{(t - t_n)(t - t_{n + 1})}\right|dt} = \frac{{\max \left|{f^{\prime\prime}(\xi )}\right|}}{{12}}{\tau}^3 .$

Погрешность для всего отрезка [a, b] будет следующей $(\tau = (b - a)(N, t_{m} = n\tau )$ :

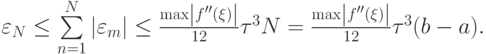
$\varepsilon_N \le \sum\limits_{n = 1}^{N}{\left|{\varepsilon_m}\right|} \le \frac{{\max \left|{f^{\prime\prime}(\xi )}\right|}}{{12}}{\tau}^3 N = \frac{{\max \left|{f^{\prime\prime}(\xi )}\right|}}{{12}}{\tau}^3 (b - a).$
Получить квадратурную формулу Гаусса для двух узлов на отрезке $t \in [- 1, 1].$
Решение. В случае двух узлов N = 1 (количество отрезков разбиения), M = 2, N + 1 = 3 (степень полинома). Узлы t_n и веса C_n должны удовлетворять следующей системе уравнений:

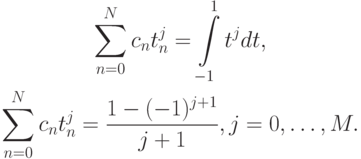
$\begin{gather*} \sum\limits_{n = 0}^{N}{c_n t_n^{j}} = \int\limits_{- 1}^1 {t^{j} dt}, \\ \sum\limits_{n = 0}^{N}{c_n t_n^{j}} = \frac{1 - (- 1)^{j + 1}}{j + 1}, j = 0, \ldots , M. \end{gather*}$

В данном случае система уравнений будет:

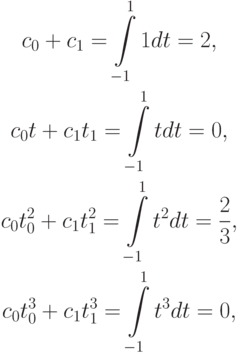
$\begin{gather*} c_0 + c_1 = \int\limits_{- 1}^1 {1 dt} = 2, \\ c_0 t + c_1 t_1 = \int\limits_{- 1}^1 {t dt} = 0, \\ c_0 t_0^2 + c_1 t_1^2 = \int\limits_{- 1}^1 {t^2 dt} = \frac{2}{3}, \\ c_0 t_0^3 + c_1 t_1^3 = \int\limits_{- 1}^1 {t^3 dt} = 0, \end{gather*}$

откуда получим

$c_0 = c_1 = 1\quad t_0 = t_1 = \frac{1}{\sqrt{3}} . $$
Формула Гаусса записывается как

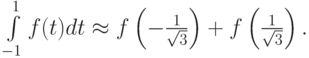
$\int\limits_{- 1}^1 {f(t)dt} \approx f\left({- \frac{1}{\sqrt{3}}}\right) + f\left({\frac{1}{\sqrt{3}}}\right) .$

Эта формула будет точной для полиномов третьей степени.
Предложить способ вычисления интеграла
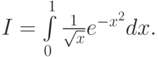
$I = \int\limits_0^1 {\frac{1}{\sqrt{x}}e^{- x^2 } dx.}$

Решение. Представим интеграл I как сумму двух интегралов

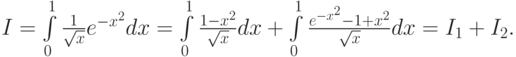
$I = \int\limits_0^1 {\frac{1}{\sqrt {x}} e^{- x^2 } d x} = \int\limits_0^1 {\frac{1 - x^2}{\sqrt {x}}dx} + \int\limits_0^1 {\frac{e^{- x^2 } - 1 + x^2}{\sqrt {x}}dx} = I_1 + I_2 .$

Первый интеграл I₁ вычисляется аналитически: I₁ = 1, 6. Поскольку подынтегральная функция в I₂ трижды непрерывно дифференцируема и ограничена, то I₂ можно вычислить, например, по формуле прямоугольников с центральной точкой:

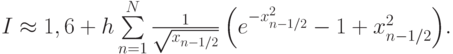
$I \approx 1, 6 + h\sum\limits_{n = 1}^{N}{\frac{1}{\sqrt{x_{n - 1/2}}}\left({e^{- x_{n - 1/2}^2} - 1 + x_{n - 1/2}^2 }\right)}.$
Предложить способ уточнения приближенного значения интеграла по квадратурной формуле, при вычисленных значениях этого интеграла при двух шагах интегрирования: h и h/2 ( правило Рунге ).
Решение. Интеграл I может быть представлен в виде

$I = I^{p} (h) + Ch^{p}; I = I^{p}\left({\frac{h}{2}}\right) + 2C_1\left({\frac{h}{2}}\right)^{p},$

где I^p(h) — приближенные значения интеграла, вычисленные по формуле с порядком точности p с шагом h,
$I^{p} \left({\frac{h}{2}}\right)$
- значение интеграла, вычисленное по той же формуле с шагом вдвое меньшим. При малых h константы C и C₁ близки. Этот факт тоже необходимо доказывать. Доказательство труда не представляет — пользуясь теоремой Лагранжа о среднем, легко получить, что эти величины отличаются на O(h_p). Тогда получим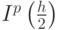

$I^{p} (h) + Ch^{p} = I^{p} \left({\frac{h}{2}}\right) + 2C_1\left({\frac{h}{2}}\right) \approx I^{p} \left({\frac{h}{2}}\right) + 2C\left({\frac{h}{2}}\right)^{p},$

откуда следует

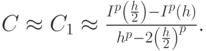
$C \approx C_1 \approx \frac{{I^{p} \left({\frac{h}{2}}\right) - I^{p}(h)}}{{h^{p} - 2\left({\frac{h}{2}}\right)^{p}}}.$

Подставив C во вторую формулу для вычисления I(c, h/2), получим:

$I \approx I^{p} \left({\frac{h}{2}}\right) + \frac{{2^{p - 1} I^{p}\left({\frac{h}{2}}\right) - I^{p} (h)}}{{2^{p - 1} - 1}}.$

Во - первых, эта простая формула позволяет относительно дешевым способом уточнить вычислительное значение интеграла с шагом h/2. Во - вторых, получаем возможность контролировать точность численного интегрирования путем вычисления значения интеграла дважды (с шагами h и h/2 ).

Примечание. Легко получается аналог правила Рунге при вычислении интеграла для табличной функции. Необходимо лишь с использованием одних и тех же квадратурных формул вычислить интеграл с шагом таблицы h и затем повторить вычисления, выкинув половину точек, с шагом 2h.