НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 8: Численное интегрирование

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3916 / 1197 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

7.5. Вычисление интегралов от функций с особенностями

Пусть требуется вычислить несобственный интеграл

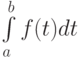
$\int\limits_{a}^{b}{f(t)dt}$

от функции, обращающейся в бесконечность в некоторой точке $c \in \left[{a, b}\right].$ В этом случае интеграл обычно разбивают на два

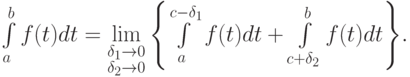
$\int\limits_{a}^{b}{f(t)dt = \lim\limits_{\substack{\delta_1 \to 0 \\ \delta_2 \to 0 }} \left\{{\int\limits_{a}^{c - \delta_1 }{f(t)dt + \int\limits_{c + \delta_2 }^{b}{f(t)dt}} }\right\}}.$

Числа $\delta_1$ и $\delta_2$ выбирают малыми величинами так, чтобы выполнялась оценка:

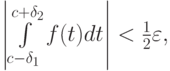
$\left|{\int\limits_{c - \delta_1 }^{c + \delta_2 }{f(t)dt}}\right| < \frac{1}{2}\varepsilon ,$

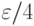где $\varepsilon$ — заданное малое положительное число (точность вычисления интеграла). После этого по квадратурным формулам вычисляют определенные интегралы $I_1 = \int\limits_{a}^{c - \delta_1} f(t)dt$ и $I_2 = \int\limits_{c + \delta_2 }^{b}{f(t) dt}$ с точностью $\varepsilon /4$ каждый. После таких вычислений за приближенное значение интеграла с особенностью принимают 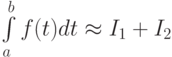$\int\limits_{a}^{b}{f(t)dt \approx I_1 + I_2}$ (с точностью $\varepsilon$ ).

Другой способ вычисления интеграла от функции особенностью, называемый методом Канторовича выделения особенностей, состоит в следующем. Представим подынтегральную функцию в виде суммы:

$\int\limits_{a}^{b}{f(t)dt = \int\limits_{a}^{b}{g(t)dt} + \int\limits_{a}^{b}{\left[{f(t) - g(t)}\right] dt.}}$

При этом g(t) подбирают так, чтобы она была интегрируемой, а разность [f(t) - g(t)] — ограниченной.

Пример. Пусть необходимо вычислить

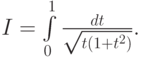
${I} = \int\limits_0^1 {\frac{dt} {{\sqrt {t(1 + t^2 )}}}}.$

Представим I как сумму двух интегралов I = I₁ + I₂, где

$I_1 = \int\limits_0^1 \frac{dt}{\sqrt{t}}, I_2 = \int\limits_0^1 [\frac{1}{\sqrt{t(1 + t^2)}} - \frac{1}{\sqrt{t}}]dt .$

Интеграл I₁ вычисляется аналитически, а I₂, поскольку подынтегральная функция ограничена, можно вычислить по квадратным формулам.

Аналогично можно поступить и в следующей задаче:

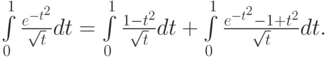
$\int\limits_0^1 {\frac{e^{- t^2 }}{\sqrt{t}}} dt = \int\limits_0^1 {\frac{1 - t^2 }{\sqrt{t}}dt + \int\limits_0^1 {\frac{e^{- t^2 } - 1 + t^2 }{\sqrt{t}}dt}.$

Интегрирование быстро осциллирующих функций типа 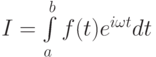$I = \int\limits_{a}^{b}{f(t)e^{i\omega t}}dt$ можно проводить, заменив f(t) на интерполяционный полином, 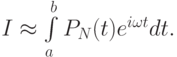$I \approx \int\limits_{a}^{b} P_N (t)e^{i\omega t}dt.$ Этот интеграл вычисляется явно.

7.6. Идея метода Монте - Карло

Метод Монте - Карло используется, как правило, для вычисления кратных интегралов. Рассмотрим задачу вычисления интеграла по многомерному кубу:

$I = \int\limits_0^1 \int\limits_0^1 \ldots \int\limits_0^1 f(t_1, t_2, \ldots , t_n)dt_1dt_2 \ldots dt_n.$

Для его вычисления можно построить кубатурные формулы, используя процедуру последовательного интегрирования, заменяя кратный интеграл I на

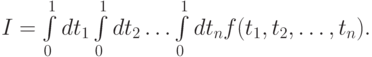
$I = \int\limits_0^1 dt_1 \int\limits_0^1 dt_2 \ldots \int\limits_0^1 dt_n f(t_1, t_2, \ldots , t_n).$

Проблема вычисления подобных интегралов заключается в том, что при росте размерности задачи объем вычисления значительно увеличивается, а задача численного интегрирования превращается из довольно простой в одну из самых сложных и трудоемких. По этой причине приведенные выше квадратурные формулы используются обычно для решения одно - , дву - и трехмерных задач.

Для вычисления интегралов по гиперкубу высокой размерности обычно используется метод Монте - Карло. Суть его состоит в том, что генерируется последовательность случайных точек единичного n - мерного куба $t_1, t_2, \ldots , t_n \in R^{n}$ ; очевидно, что чем больше точек участвует в вычислительном процессе, тем больше точность расчета.

Пусть теперь необходимо взять интеграл по области $\Omega,$ принадлежащей n - мерному кубу, причем, $\Omega$ выделяется неравенствами

$g_j (t_k) \le 0, \quad j = 1 \div J, \quad k = 1 \div K.$

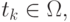Далее генерируется последовательность случайных чисел, равномерно распределенная в единичном гиперкубе, и для всех точек проверяются неравенства $g_j (t_k) \le 0.$ Если они выполнены, т.е. $t_k \in \Omega,$ то вычисляются значения f(t_k), прибавляющиеся к сумме.

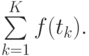
Пусть вычислено M точек, из которых {K} попали в $\Omega$ и накоплена сумма $\sum\limits_{k = 1}^{K}{f(t_k)}.$

Среднее по объему $\Omega$ значение функции f вычисляется по формуле

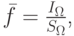
$$ \bar{f} = \frac{I_{\Omega}}{S_{\Omega}} $,$

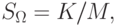
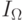где $S_{\Omega } = K/M,$ $I_{\Omega }$ — кратный интеграл по $\Omega.$

С другой стороны, это же значение можно приближенно вычислить как сумму:

$\left[{\sum {f(t_k)}}\right]/K.$

Приравнивая эти выражения, получим:

$\frac{M}{K}I_\Omega \approx \frac{1}{K}\sum\limits_{k = 1}^{K}{f(t_k)}, \mbox{откуда } I_\Omega \approx \frac{1}{M}\sum\limits_{k = 1}^{K}{f(t_k)} .$

Дальше >>

Авторизоваться

Введение в вычислительную математику

Численное интегрирование

7.5. Вычисление интегралов от функций с особенностями

7.6. Идея метода Монте - Карло

Вопросы и ответы