Введение в вычислительную математику
[+]
Московский физико-технический институт
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3914 / 1195 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00
ISBN: 978-5-9556-0065-9
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Программист, Математик
Теги: beta, алгебра, алгоритмы, арифметика, вычисления, дифференциальные уравнения, курсы, линейная алгебра, матрица Якоби, метод трапеций, метод Эйлера, норма вектора, поиск, программирование, разделенные разности, разложение в ряд, системы нелинейных уравнений, спектральные задачи, таблицы бутчера, численное решение уравнений, элементы
Лекция 8:

Численное интегрирование
A
|
версия для печати
< Лекция 7 || Лекция 8: 12345678 || Лекция 9 >

Формула Симпсона. Заменим подынтегральную функцию f(t) на отрезке [tk - 1, tk] интерполяционным полиномом (в форме Лагранжа) второй степени. Для простоты положим 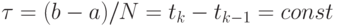\tau = (b - a)/N = t_{k} - t_{k - 1} = const для всех k — сетка на отрезке интегрирования равномерная. Тогда

\begin{gather*} F(t) = f_{k - 1} \frac{{(t - t_{k - 1/2})(t - t_k)}}{{(t_{k - 1} - t_{k - 1/2})(t_{k - 1} - t_k)}} + f_{k - 1/2}\frac{{(t - t_{k - 1})(t - t_k)}}{{(t_{k - 1/2} - t_{k - 1})(t_{k - 1/2} - t_k)}} + \\ + f_k \frac{{(t - t_{k - 1})(t - t_{k - 1/2})}}{{(t_k - t_{k - 1})(t_k - t_{k - 1/2})}} = \frac{2}{{{\tau}^2 }}\left[(t - t_{k - 1/2})(t - t_k)f_{k - 1} -\right. \\ \left. - 2(t - t_{k - 1})(t - t_{k - 1/2})f_{k - 1/2} + (t - t_{k - 1})(t - t_{k - 1/2})f_k\right] . \end{gather*}

После вычисления интеграла от полинома получим приближенное значение интеграла по элементарному отрезку

$ I_k \approx \frac{{\tau}}{6}\left[{f_{k - 1} + 4f_{k - 1/2} + f_k}\right]. $

Суммируя по всем элементарным отрезкам [tk - 1, tk], получим

\begin{gather*} I \approx \frac{{\tau}}{6}\sum\limits_{k = 1}^{N}{\left[{f_{k - 1} + 4f_{k - 1/2} + f_k}\right]} = \\ = \frac{{\tau}}{6}\left({f_0 + 4f_{1/2} + 2f_1 + 4f_{3/2} + \ldots + 2f_{N - 1} + 4f_{N - 1/2} + f_N}\right), \end{gather*}

где

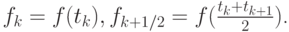
$ f_k = f(t_k), f_{k + 1/2} = f(\frac{{t_k + t_{k + 1}}}{2}) $.
Формулу Симпсона можно также записать, не используя дробных индексов:

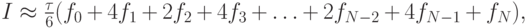
$ I \approx \frac{{\tau}}{6}(f_0 + 4f_1 + 2f_2 + 4f_3 + \ldots + 2f_{N - 2} + 4f_{N - 1} + f_N), $

если локальную формулу получать путем интегрирования интерполяционного полинома второй степени по отрезку [tk - 1, tk + 1]:

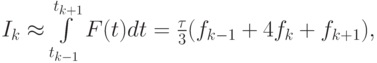
$ I_k \approx \int\limits_{t_{k - 1}}^{t_{k + 1}}F (t)dt = \frac{{\tau}}{3}(f_{k - 1} + 4f_k + f_{k + 1}), $

где F(t) — интерполяционный полином, построенный на отрезке [tk - 1, tk + 1] по точкам tk - 1, tk, tk + 1. В этом случае N — число разбиений отрезка на элементарные отрезки — должно быть четным.

Еще одна используемая на практике квадратурная формула интерполяционного типа — так называемое "правило 3/8". Она получается при замене подынтегральной функции интерполяционным полиномом третьей степени, построенным по четырем точкам. Расчетные формулы для правила 3/8 приведем без вывода:

$ \int\limits_{a}^{b}{f(t)} dt \approx (b - a)\left[{\frac{1}{8}f(a) + \frac{3}{8}f\left({\frac{{2a + b}}{3}}\right) + \frac{3}{8}f\left({\frac{{a + 2b}}{3}}\right) + \frac{1}{8}f(b)}\right] . $

Квадратурные формулы интерполяционного типа более высокого порядка применяются достаточно редко.

Конечно, существуют и формулы интерполяционного типа более высоких порядков. Они не применяются на практике по следующим обстоятельствам. Любая формула интерполяционного типа записывается в виде

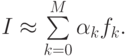
I \approx \sum\limits_{k = 0}^{M}{\alpha_k f_k}.

Во всех приведенных выше формулах коэффициенты \alpha_k были положительными. Такие квадратурные формулы называются правильными квадратурными формулами. При использовании полиномов более высоких степеней получаются квадратурные формулы, не являющиеся правильными.

Для степени интерполяционного полинома более 7 среди коэффициентов встречаются отрицательные. Д.Пойа показал, что

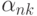\lim\limits_{n \to \infty } \sum\limits_{k = 0}^{n}{\left|{\alpha_{nk}}\right|} = \infty,

где \alpha_{nk} — веса квадратурной формулы, получающейся при замене подынтегрального выражения интерполяционным полиномом степени n. Такое увеличение суммы абсолютных значений коэффициентов связано с быстрым ростом постоянной Лебега при алгебраической интерполяции на равномерной сетке.

Подробнее о свойствах квадратурных формул интерполяционного типа можно прочитать в [7.6].

Дальше >>
< Лекция 7 || Лекция 8: 12345678 || Лекция 9 >

Вопросы и ответы

вопросов: 1
Sanjar Ibrohimov
Sanjar Ibrohimov
ответить