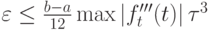НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 8: Численное интегрирование

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3791 / 1086 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 53 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

7.2. Оценка погрешности квадратурных формул

Погрешность квадратурных формул может быть оценена, например, с использованием остаточного члена интерполяционного полинома:

$\varepsilon_k = \left|\int\limits_{t_k}^{t_{k + 1}}R_N(t) dt\right| \le \frac{\max\limits_{[t_k, t_{k + 1}]}\left|f^{(N + 1)}(\xi)\right| }{(N + 1)!} {\tau}\max\limits_{[t_k, t_{k + 1}]}\left|{\mathop \Pi\limits_{k = 0}^{N}(t - t_k)}\right|.$

Из последней формулы следует, что квадратурная формула точна, если подынтегральная функция является многочленом степени не выше N.

Получим, например, локальную оценку погрешности для формулы трапеций, используя формулу для остаточного члена интерполяционного полинома 1 - го порядка:

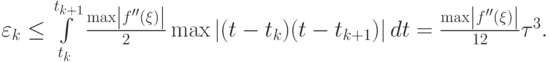
$\varepsilon_k \le \int\limits_{t_k}^{t_{k + 1}}{\frac{{\max \left|{f^{\prime\prime}(\xi )}\right|}}{2}} \max \left|{(t - t_k)(t - t_{k + 1})}\right|dt = \frac{{\max \left|{f^{\prime\prime}(\xi )}\right|}}{{12}}\tau^3 .$

Тогда погрешность по всему отрезку [a, b] будет составлять

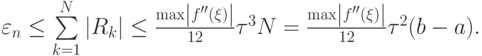
$\varepsilon_n \le \sum\limits_{k = 1}^{N}{\left|{R_k}\right|} \le \frac{{\max \left|{f^{\prime\prime}(\xi )}\right|}}{12}{\tau}^3 N = \frac{{\max \left|{f^{\prime\prime}(\xi )}\right|}}{12}{\tau}^2 (b - a).$

Другой способ получения погрешности квадратурных формул состоит в следующем. Рассмотрим интеграл по элементарному отрезку

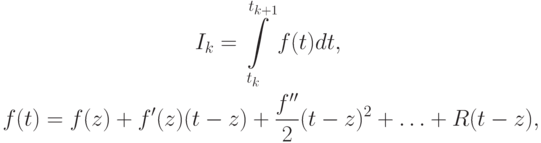
$\begin{gather*} I_k = \int\limits_{t_k}^{t_{k + 1}}{f(t)}dt, \\ f(t) = f(z) + f^{\prime}(z)(t - z) + \frac{{f^{\prime\prime}}}{2}(t - z)^2 + \ldots + R(t - z), \end{gather*}$

где $z \in \left[{t_k , t_{k + 1}}\right]$ — некая опорная точка, тогда для приближенного значения интеграла верно

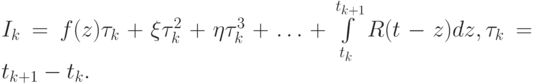
$I_k = f(z)\tau_k + \xi\tau^2_k + \eta\tau^3_k + \ldots + \int\limits_{t_k}^{t_{k + 1}} R(t - z)dz, \tau_k = t_{k + 1} - t_k.$

Коэффициенты $\xi , \eta , ...$ зависят от производных f'(z), f''(z), ....

С другой стороны, любая из рассмотренных квадратурных формул представима в виде

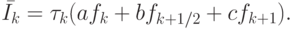
$\bar {I_k} = \tau_k (af_k + bf_{k + 1/2} + cf_{k + 1}).$

Заменяя в этой формуле значения функций f в точках f_k, f_{k + 1/2}, f_{k + 1} ее разложением по формуле Тейлора, получим

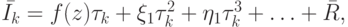
$\bar {I_k} = f(z)\tau_k + \xi_1 \tau_k^2 + \eta_1 \tau_k^3 + \ldots + \bar {R},$

где $z \in [t_k, t_{k + 1} ].$

Сравнивая разложения для 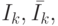$I_k, \bar {I_k},$ легко заметить, что вместе с первым слагаемым совпадают и другие слагаемые до (m - 1) - го порядка, так что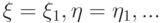 $\xi = \xi _{1}, \eta = \eta _{1}, ...$

Разность же несовпадающих слагаемых будет, очевидно, оценкой погрешности квадратурной формулы на интервале $[t_k, t_{k + 1} ]: \varepsilon_k = \left|I_k - \bar {I_k}\right| \le v \max\limits_{[t_k, t_{k + 1}]}\left|f^ {(m)}\right| \tau^{m + 1}_k,$ где v — константа.

Если просуммировать локальные погрешности по всем интервалам [ t_k, t_{k + 1} ], то получим оценку погрешности квадратурной формулы по всему отрезку [a, b]:

$\varepsilon = \left|I - \bar {I}\right| \le v(b - a)\max\limits_{[a, b]} \left|f^ {(m)}\right| \tau^{m},$

где ${\tau}= \max\limits_k \tau_k$ на неравномерной сетке, или $\tau = (b - a)/N$ на равномерной. Число m называется порядком точности квадратуры.

Получим теперь погрешность формулы прямоугольников (со средней точкой) для $\tau _{k} = \tau = const$ :

$\varepsilon \le \frac{b - a}{24} \max\limits_{[a, b ]}\left|{f^{\prime\prime}_{t} (t)}\right|{\tau}^2,$

погрешность формулы трапеций

$\varepsilon \le \frac{b - a}{12} \max\limits_{[a, b]}\left|{f^{\prime\prime}_{t} (t)}\right|{\tau}^2,$

погрешность формул Симпсона (с дробными и без дробных индексов соответственно)

$\begin{multiple} \varepsilon \le \frac{b - a}{2880}\max\limits_{[a, b]} \left|{f_{t}^{(4)} (t)}\right|{\tau}^4, \\ \varepsilon \le \frac{{b - a}}{{180}}\max\limits_{[a, b]} \left|{f_{t}^{(4)} (t)}\right|{\tau}^4 \end{multiple)$

Заметим, что если функция f(t) имеет только три непрерывных производных, то оценка погрешности формулы Симпсона ухудшается на порядок:

$\varepsilon \le \frac{b - a}{12} \max\left|f^{\prime\prime\prime}_{t} (t)\right|\tau^3$

Дальше >>

Авторизоваться

Введение в вычислительную математику

Численное интегрирование

7.2. Оценка погрешности квадратурных формул

Вопросы и ответы