Московский физико-технический институт
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3914 / 1195 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00
ISBN: 978-5-9556-0065-9
Специальности: Программист, Математик
Теги:
Лекция 8:
Численное интегрирование
7.3. Кратные интегралы
Рассмотрим, для примера двукратный интеграл по прямоугольной области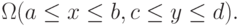 
Аналогично одномерному случаю, в соответствии с формулой прямоугольников (со средней точкой) заменим функцию
ее значением в точке пересечения диагоналей прямоугольника. В таком случае получим
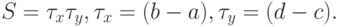Если разбить прямоугольник на прямоугольные ячейки Si, то получим аналог формулы прямоугольников со средней точкой в виде суммы по i: 
где Si — площадь i - ой прямоугольной ячейки, xi, yi — координаты точки пересечения ее диагоналей.Применим теперь формулу Симпсона для вычисления двукратного интеграла путем редукции к методу вычисления одномерного интеграла, зачем представим двойной интеграл как
Сначала применим формулу Симпсона для вычисления внешнего интеграла:
![$ I \approx \frac{{\tau_x}}{6}\left[{\int\limits_{c}^{d}{f(a, y)} dy + 4\int\limits_{c}^{d}{f(\frac{{a + b}}{2}, y) dy + \int\limits_{c}^{d}{f(b, y) dy}} }\right] . $](/sites/default/files/tex_cache/d07e774c6f7d6045771dada09df81c51.png)
Теперь применим формулу Симпсона для каждого из трех полученных интервалов:
![\begin{gather*}
I_1 = \int\limits_{c}^{d} f(a, y) dy \approx \frac{\tau_y}{6} \left[f(a, c) + 4f(a, \frac{c + d}{2}) + f(a, d)\right], \\
I_2 = \int\limits_{c}^{d} f(\frac{a + b}{2}, y) dy \approx \frac{\tau_y}{6}\left[f(\frac{a + b}{2}, c) + 4f(\frac{a + b}{2}, \frac{c + d}{2}) + f(\frac{a + b}{2}, d)\right], \\
I_3 = \int\limits_{c}^{d} f(b, y) dy \approx \frac{\tau_y}{6} \left[f(b, c) + 4f(b, \frac{c + d}{2}) + f(b, d)\right]
\end{gather*}](/sites/default/files/tex_cache/8814a66f5ccd571d1005de2a48a36f7f.png)
Подставляя приближенные формулы для вычисления интегралов I1, I2, I3 в формулу для вычисления i, получим
![\begin{gather*}
I \approx \frac{{\tau_x \tau_y}}{{36}}\left\{{f(a, c) + f(a, d) + f(b, c) + f(b, d) + }\right. \\
\left. {+ 4\left[{f(a, \frac{{c + d}}{2}) + f(b, \frac{{c + d}}{2}) + f(\frac{{a + b}}
{2}, c) + f(\frac{{a + b}}{2}, d)}\right] + 16f\left({\frac{{a + b}}{2}, \frac{{c + d}}
{2}}\right)}\right\}
\end{gather*}](/sites/default/files/tex_cache/6e0a6c470c71527fc8d188d9e4b5f44e.png)
Если область интегрирования не является прямоугольной, то ее можно сделать
подобластью большей по площади прямоугольной области, которую в свою очередь разбить на прямоугольные ячейки. Ячейки в этом случае разделяются на внутренние, к ним применяются приведенные формулы численного интегрирования, и граничные, не прямоугольные, площади которых вычисляются по более сложным алгоритмам. При этом приближенное значение интеграла, например, при использовании формулы средних, можно записать как 
где 
— приближенное значение интегралов по внутренним ячейкам,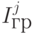 
— по граничным, i, j — номера ячеек с площадями Si и Sj.
7.4. Квадратурные формулы Гаусса
Поскольку формулы Ньютона - Котеса являются интерполяционными, очевидно, что они не могут успешно использоваться для получения формул высокой точности по причине неустойчивости интерполяционного процесса для многочленов высокого порядка. Как отмечалось выше, постоянные Лебега растут с увеличением количества узлов интерполяции для равномерной сетки как 2N. По этой причине обычно используются полиномы степени от нуля до трех (соответственно, формулы прямоугольников со средней точкой, трапеций, Симпсона, 3/8). Вычисление с их помощью интегралов от функций, обладающих высокой степенью гладкости, например, близким к полиномам высокой степени, представляется нерациональным. В выражение для погрешности этих формул входят первая, вторая или четвертая производные. Погрешность определяется низким порядком производной при высокой степени гладкости интегрируемой функции. Этих недостатков лишены квадратуры Гаусса.
Формулировка задачи построения квадратурных формул, поставленная Гауссом, такова.
Для заданного количества точек, а именно, для (N + 1) точки, найти такое расположение узлов и такие веса ci, чтобы квадратурная формула
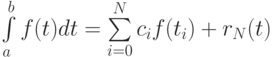
была точной для полиномов как можно более высокой степени, т.е. чтобы rN(t) = 0.
