НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 7: Интерполяция функций

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3914 / 1195 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

6.11. B - сплайны

Сплайны с локальным носителем. ( B - сплайны ). В последнее время в вычислительной практике широкое распространение получили B - сплайны (от английского слова bell — колокол), сосредоточенные на конечном носителе. Они используются как для интерполяции функций, так и в качестве базисных функций при построении методов типа конечных элементов.

Для подробного ознакомления с приложениями B - сплайнов и B - сплайнами произвольной степени рекомендуется обратиться к [6.5], [6.6] и современным публикациям, например, в журнале "Математическое моделирование" [6.14]. В "Интерполяция функций" ограничимся наиболее распространенными случаями B - сплайнов порядка 2 и 3, см. также [6.11].

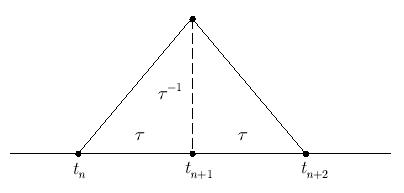
Определение. B - сплайном, или базисным сплайном степени N - 1 дефекта 1 относительно узлов $\left\{{t_i}\right\}_{i = n}^{n + N}$ называется функция

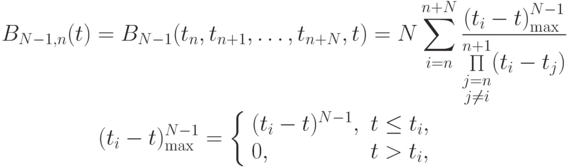
$\begin{gather*} B_{N - 1, n} (t) = B_{N - 1}(t_n, t_{n + 1}, \ldots , t_{n + N}, t) = N \sum\limits_{i = n}^{n + N}\frac{{\left({t_i - t}\right)}^{N - 1}_{\max}}{\mathop{\Pi}\limits^{n + 1}_{\substack{ j = n \\ j \ne i}} (t_i - t_j)} \\ (t_i - t)^{N - 1}_{\max} = \left\{ \begin{array}{ll} (t_{i} - t)^{N - 1}, & t \le t_i, \\ 0, & t > t_i, \\ \end{array} \right. \end{gather*}$

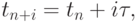Пусть $t_{n + i} = t_{n} + i\tau ,$ т.е. рассматривается случай равномерной сетки.

Рассмотрим несколько частных случаев В - сплайнов.

N = 2. В этом случае сплайн строится наиболее просто.
$\begin{gather*} B_{1, n} (t) = B_1(t_n, t_{n + 1}, t_{n + 2}, t) = 2\left[\frac{{(t_n - t)_{\max }}}{{(t_n - t_{n + 1})(t_n - t_{n + 2})}} +\right. \\ \left. \frac{{(t_{n + 1} - t)_{\max }}}{{(t_{n + 1} - t_n)(t_{n + 1} - t_{n + 2})}} + \frac{{(t_{n + 2} - t)_{\max }}}{{(t_{n + 2} - t_n)(t_{n + 2} - t_{n + 1})}}\right] = \\ = \frac{1}{{\tau ^2 }}\left[(t_n - t)_{\max } - 2(t_{n + 1} - t)_{\max } + (t_{n + 2} - t)_{\max }\right], \end{gather*}$

или

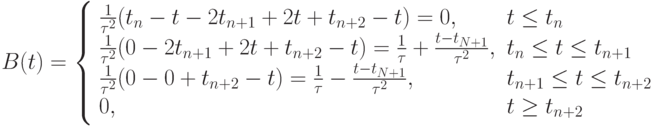
$B(t) = \left\{ \begin{array}{ll} \frac {1}{\tau^2}(t_n - t - 2t_{n + 1} + 2t + t_{n + 2} - t) = 0, & t \le t_n \\ \frac {1}{\tau^2}(0 - 2t_{n + 1} + 2t + t_{n + 2} - t) = \frac {1}{\tau} + \frac {t - t_{N + 1}}{\tau^2}, & t_n \le t \le t_{n + 1} \\ \frac {1}{\tau^2}(0 - 0 + t_{n + 2} - t) = \frac {1}{\tau} - \frac {t - t_{N + 1}}{\tau^2}, & t_{n + 1} \le t \le t_{n + 2} \\ 0, & t \ge t_{n + 2} \\ \end{array} \right.$

Это функция "крышка" или "крышечка". Она часто используется в качестве базисной функции в методах конечных элементов.

Рассмотрим случай B - сплайна 2 - го порядка, задаваемого формулой

$S_k (x) = \left\{ \begin{array}{lll} {x^2 ;} & {x = \frac{t - t_{k - 2}}{t_{k - 1} - t_{k - 2}}, } & {t \in [t_{k - 2}, t_{k - 1} ];} \\ {1 + 2x - x^2 ;} & {x = \frac{t - t_{k - 1}} {t_k - t_{k - 1}}, } & {t \in [t_{k - 1}, t_k ];} \\ {2 - x^2 ;} & {x = \frac{t - t_k}{t_{k + 1} - t_k}, } & {t \in [t_k , t_{k + 1} ];} \\ {(1 - x)^2 ;} & {x = \frac{t - t_{k + 1}}{t_{k + 2} - t_{k + 1}}, } & {t \in [t_{k + 1}, t_{k + 2} ].} \\ \end{array} \right.$

При t < t_{k - 2}, t > t_{k - 2}, $S_k (x) \equiv 0.$ Построенный сплайн обладает следующими свойствами:
- a) S'_t (t_{k - 2}) = S'_t(t_{k + 2}) = 0 ;
- b) S(t_{k - 1}) = S(t_{k + 1}) = 1 ;
- c) S(t_{k - 2}) = S(t_{k + 2}) = 0.
При интерполяции функций можно поступить таким способом. Заметим, что для интерполяции с помощью сплайна необходимо потребовать выполнения условия
```
b_{i - 1}S_{i - 1} + b_iS_i + b_{i + 1}S_{i + 1}= f_i,
```
где b — коэффициенты интерполяции, S — B - сплайн, индекс указывает на точку носителя, в которой сплайн достигает своего максимума. Система таких соотношений, естественно, дополняется граничными условиями. Известно [6.5], что получившаяся система для определения коэффициентов разложения будет иметь трехдиагональную матрицу с диагональным преобладанием при выполнении ограничения на длины соседних шагов: они должны различаться не более чем в
$\frac{1 + \sqrt{13}}{2}$
раза.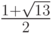
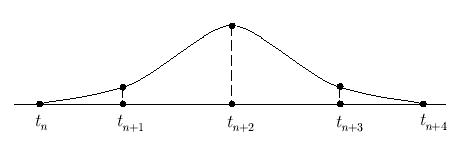
N = 4 (кубический B - сплайн ) имеет вид
$\begin{gather*} B_{3, n}(t) = \frac{1}{{6\tau ^4 }}\left[(t_n - t)_{\max }^3 - 4(t_{n + 1} - t)_{\max }^3 + 6(t_{n + 2} - t)_{\max }^3 -\right. \\ \left. - 4(t_{n + 3} - t)_{\max }^3 + (t_{n + 4} - t)_{\max }^3\right], \end{gather*}$

или, после несложных упрощений:

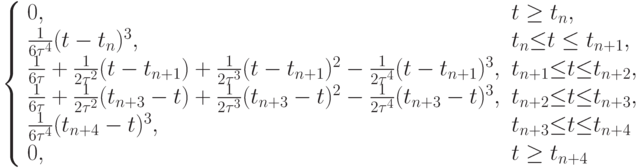
$\left\{ \begin{array}{ll} 0, & {t \ge t_n, } \\ {\frac {1}{6\tau^4}(t - t_n)^3, } & {t_n{\le} t \le t_{n + 1}}, \\ {\frac {1}{6\tau} + \frac {1}{2\tau^2}(t - t_{n + 1}) + \frac{1}{2\tau^3}(t - t_{n + 1})^2 - \frac {1}{2\tau^4}(t - t_{n + 1})^3, } & {t_{n + 1}{\le} t {\le} t_{n + 2}, } \\ {\frac{1}{6\tau} + \frac{1}{2\tau^2}(t_{n + 3} - t) + \frac{1}{2\tau^3}(t_{n + 3} - t)^2 - \frac{1}{2\tau^4}(t_{n + 3} - t)^3, } & {t_{n + 2}{\le} t {\le} t_{n + 3}, } \\ {\frac{1}{6\tau^4}(t_{n + 4} - t)^3, } & {t_{n + 3}{\le} t {\le} t_{n + 4}} \\ {0, } & {t \ge t_{n + 4}} \\ \end{array} \right.$

Базисные сплайны заданной степени являются линейно независимыми функциями и образуют базис в функциональных пространствах, что можно использовать для представления с их помощью других функций этих же пространств. Любая, например, кусочно - постоянная функция на отрезке, составленном из равных интервалов, может быть единственным образом представлена как линейная комбинация В - сплайнов нулевой степени, любая кусочно - линейная функция — В - сплайнов первой степени и т.д. Базисные сплайны играют существенную роль при построении численных методов решения задач математической физики, например, метода конечных элементов в теории приближения функций, при решении задач компьютерной графики.

Для последнего класса задач также используются функции Бернштейна:

$\begin{gather*} B_n^{N} (t) = \frac{N!}{n!(N - n)!}\frac{{(b - t)}^{N - n}{(t - a)}^{n}}{{(b - a)}^{N}}, \\ n = 0, \ldots , N, t \in [a, b]. \end{gather*}$

Функции Бернштейна иногда записывают в форме рекуррентного соотношения:

$\begin{gather*} B_{- 1}^{N} (t) = 0, B_0^0 (t) = 1, B_i^{N} (t) = \frac{{(b - t)B_i^{N - 1} (t) + (t - a)B_{i - 1}^{N - 1}(t)}}{{b - a}}, \\ i = 0, \ldots , n, B_{N + 1}^{N} (t) = 0. \end{gather*}$

Такие рекуррентные последовательности применяются с целью уменьшения ошибок округления.

Функции Бернштейна являются базисными для построения кривых Безье, активно использующихся в компьютерной графике и техническом дизайне, появившихся в результате работ Безье и де Кастильо над формами автомобилей фирм Рено и Ситроен. Подробнее о функциях Бернштейна в [6.12].