НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 7: Интерполяция функций

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3914 / 1195 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

6.3. Интерполяция обобщенными полиномами

Для того чтобы функция ( обобщенный полином )

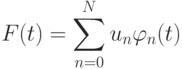
$F(t) = \sum\limits_{n = 0}^{N}{u_n \varphi_n (t)}$

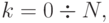была интерполирующей, необходимо выполнение условий: F(t_k) = f_k, $k = 0 \div N,$ где f_k — значения функции в точках интерполяции. Для коэффициентов обобщенного полинома получаем систему уравнений: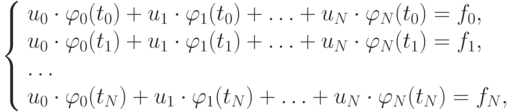

$\left\{ \begin{array}{l} u_0 \cdot \varphi_0 (t_0 ) + u_1 \cdot \varphi_1 (t_0 ) + \ldots + u_N \cdot \varphi_N (t_0 ) = f_0, \\ u_0 \cdot \varphi_0 (t_1 ) + u_1 \cdot \varphi_1 (t_1 ) + \ldots + u_N \cdot \varphi_N (t_1 ) = f_1, \\ \ldots \\ u_0 \cdot \varphi_0 (t_N) + u_1 \cdot \varphi_1 (t_N) + \ldots + u_N \cdot \varphi_N (t_N) = f_N , \\ \end{array} \right.$

или в векторной форме

${\mathbf{Au}} = {\mathbf{f}},$

где

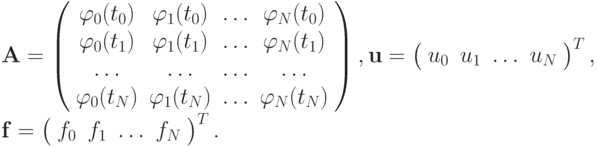
${\mathbf{A}} = \left( \begin{array}{cccc} {\varphi_0 (t_0 )} & {\varphi_1 (t_0 )} & \ldots & {\varphi_N (t_0 )} \\ {\varphi_0 (t_1 )} & {\varphi_1 (t_1 )} & \ldots & {\varphi_N (t_1 )} \\ \ldots & \ldots & \ldots & \ldots \\ {\varphi_0 (t_N)} & {\varphi_1 (t_N)} & \ldots & {\varphi_N (t_N)} \\ \end{array} \right), {\mathbf{u}} = \left( \begin{array}{cccc} {u_0 } & {u_1 } & \ldots & {u_N} \\ \end{array} \right)^{T}, \\ {\mathbf{f}} = \left( \begin{array}{cccc} {f_0 } & {f_1 } & \ldots & {f_N} \\ \end{array} \right)^{T}.$

Теорема (доказывается в курсе линейной алгебры.) Для того чтобы решение задачи интерполяции существовало и было единственным, необходимо и достаточно, чтобы система базисных функций $\varphi_N (t_k)$ была линейно независима.

Теорема (доказывается в курсе линейной алгебры.) Для того чтобы система функций $\varphi_N (t_k)$ была линейной независимой в точках t₀, ..., t_n, необходимо и достаточно, чтобы определитель матрицы Грама

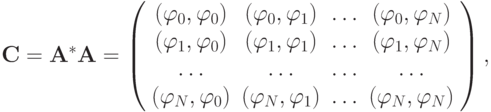
${\mathbf{C}} = {\mathbf{A}}^\ast {\mathbf{A}} = \left( \begin{array}{cccc} {(\varphi_0, \varphi_0)} & {(\varphi_0, \varphi_1)} & \ldots & {(\varphi_0, \varphi_N)}\\ {(\varphi_1, \varphi_0)} & {(\varphi_1, \varphi_1)} & \ldots & {(\varphi_1, \varphi_N)}\\ \ldots & \ldots & \ldots & \ldots \\ {(\varphi_N , \varphi_0)} & {(\varphi_N , \varphi_1)} & \ldots & {(\varphi_N , \varphi_N)} \end{array} \right),$

был отличен от нуля. Здесь каждый элемент матрицы Грама имеет вид

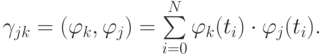
$\gamma_{jk} = (\varphi_k , \varphi_j) = \sum\limits_{i = 0}^{N}{\varphi_k (t_i) \cdot \varphi_j (t_i)}.$

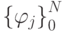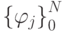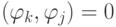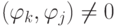В случае, если система функций $\left\{{\varphi_j}\right\}_0^{N}$ ортогональна на множестве точек $\left\{{t_j}\right\}_0^{N},$ решение задачи интерполяции значительно упрощается (напомним, что система функций $\left\{{\varphi_j}\right\}_0^{N}$ является ортогональной на множестве точек $\left\{{t_j}\right\}_0^{N},$ если $(\varphi_k , \varphi_j) = 0$ при $k \ne j$ и $\left({\varphi_k , \varphi_j}\right) \ne 0$ при k = j для всех k = 0, 1, ..., N ; j = 0, 1, ..., n ).

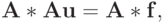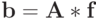Дело в том, что матрица Грама для ортогональной системы функций диагональна, и ее определитель отличен от нуля (всякая ортогональная система функций заведомо линейно независима). Линейная система уравнений представляется как ${\mathbf{A}}*{\mathbf{Au}} = {\mathbf{A}}*{\mathbf{f}},$ или $\mathbf{Cu} = \mathbf{b},$ где $\mathbf{C} = \mathbf{A}*\mathbf{A},$ $\mathbf{b} = \mathbf{A}*\mathbf{f}$ - вектор, а ее решение в случае $\mathbf{A}*\mathbf{A} = \mathbf{E}$ есть ${\mathbf{u}} = {\mathbf{A}}*{\mathbf{f}}.$

Примером ортогональной системы являются показательные функции $e^{2\pi ikt_j}$ на множестве точек t_j = {j / N}, j = 0, 1, ..., N (на отрезке [0, 1] ).

6.4. Полиномиальная (алгебраическая) интерполяция

В этом случае (u_k(t) = t^k) СЛАУ для определения коэффициентов имеет вид

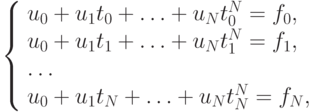
$\left\{ \begin{array}{l} u_0 + u_1 t_0 + \ldots + u_N t_0^{N} = f_0, \\ u_0 + u_1 t_1 + \ldots + u_N t_1^{N} = f_1, \\ \ldots \\ u_0 + u_1 t_N + \ldots + u_N t_N^{N} = f_N , \\ \end{array} \right.$

а ее определитель

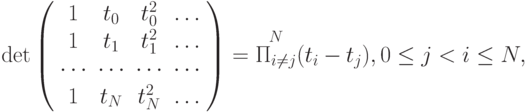
$\det \left( \begin{array}{cccc} 1 & {t_0 } & {t_0^2 } & \ldots \\ 1 & {t_1 } & {t_1^2 } & \ldots \\ \cdots & \cdots & \cdots & \cdots \\ 1 & {t_N} & {t_N^2 } & \ldots \\ \end{array} \right) = \mathop {\Pi\limits_{i \ne j}}\limits^{N}(t_i - t_j), 0 \le j < i \le N,$

отличен от нуля, если узлы интерполяции попарно различны. Это известный из курса линейной алгебры определитель Вандермонда.

Ответ на вопрос о существовании и единственности решения СЛАУ оказывается — утвердительным - решение задачи алгебраической интерполяции всегда существует и единственно, но при больших N система оказывается плохо обусловленной. Однако решение этой задачи можно выписать в явном виде

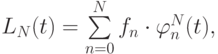
$L_N (t) = \sum\limits_{n = 0}^{N}{f_n} \cdot \varphi_n^{N} (t),$

где

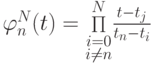
$\varphi_n^{N} (t) = {\mathop \Pi\limits^N_{\substack{i = 0 \\ i \ne n}}} \frac{t - t_j}{t_n - t_i}$

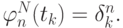- базисные функции, являющиеся полиномами степени N, каждый из которых сопоставлен со своим узлом сетки так, что $\varphi_n^{N} (t_k) = \delta_k^{n} .$ Заметим, что правильнее было бы писать L_N(t, {t_n}, {f_n}), т.е. интерполянт зависит от t, сетки и сеточной функции. Такой вид записи алгебраического интерполяционного полинома не единственен. Выписанный полином называется интерполяционным полиномом в форме Лагранжа. Он удобен для теоретического рассмотрения, но на практике часто оказывается более удобной другая форма представления — полином в форме Ньютона, о котором речь пойдет ниже.

Дальше >>

Авторизоваться

Введение в вычислительную математику

Интерполяция функций

6.3. Интерполяция обобщенными полиномами

6.4. Полиномиальная (алгебраическая) интерполяция

Вопросы и ответы