Введение в вычислительную математику
[+]
Московский физико-технический институт
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3977 / 1246 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00
ISBN: 978-5-9556-0065-9
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Программист, Математик
Теги: beta, алгебра, алгоритмы, арифметика, вычисления, дифференциальные уравнения, курсы, линейная алгебра, матрица Якоби, метод трапеций, метод Эйлера, норма вектора, поиск, программирование, разделенные разности, разложение в ряд, системы нелинейных уравнений, спектральные задачи, таблицы бутчера, численное решение уравнений, элементы
Лекция 7:

Интерполяция функций
A
|
версия для печати
< Лекция 6 || Лекция 7: 1234567891011 || Лекция 8 >

6.9. Интерполяция с кратными узлами

Определение. Пусть в узлах сетки 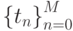\left\{{t_n}\right\}_{n = 0}^{M} заданы не только значения функции f(tn), но и значения ее производных f'(tn), f''(tn), ..., f^{(k_n - 1)}(t_n). В этом случае узел tn называется кратным, а число kn, равное количеству заданных значений производных в n узле — кратностью узла.

Доказывается теорема о существовании единственного полинома PN(t), удовлетворяющего условиям

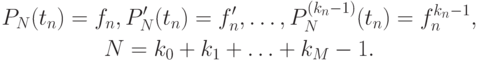
\begin{gather*} P_N (t_n) = f_n, P^{\prime}_N (t_n) = f^{\prime}_n, \ldots , P_N^{(k_n - 1)} (t_n) = f_n^{k_n - 1}, \\ N = k_0 + k_1 + \ldots + k_M - 1. \end{gather*}

Такой полином называется полиномом с кратными узлами. Отметим два частных случая.

  • в точке t = t0 заданы f0, f'0, ..., f0(N) (M = 0, k0 = N + 1).

    Тогда многочлен PN(t), удовлетворяющий этим условиям, может быть записан как

    $ P_N (t) = \sum\limits_{i = 0}^{N}{f^{(i)} (t_0 )}\frac{{(t - t_0)}^i}{i!}. $

    Это — ряд Тейлора, который является интерполянтом с кратным узлом в точке t = t0 кратности N + 1.

  • Пусть на концах отрезка [t0, t1] заданы значения f0, f1, f'0, f'1 (M = 1, k0 = 2, k1 = 2, N = 3). Тогда P3(t0) = f0, P'3(t0) = f'0, P3(t1) = f1, P'3(t1) = f'1, а интерполянт имеет вид

    \begin{gather*} P_3 (t) = f_0 \frac{{(t_1 - t)^2 \left[{2(t - t_0 ) + \tau }\right]}}{{\tau ^3 }} + {f^{\prime}}_0 \frac{{(t_1 - t)^2 (t - t_0 )}}{{\tau ^2 }} + \\ + f_1 \frac{{(t - t_0 )^2 \left[{2(t_1 - t) + \tau }\right]}}{{\tau ^3 }} + f^{\prime}_1 \frac{{(t - t_0)^2 (t - t_1 )}}{{\tau ^2 }}, \end{gather*}

    здесь \tau = t_{1} - t_{0}.

    Такой многочлен называется кубическим интерполяционным многочленом Эрмита.

Теорема (без доказательства). Пусть f(t) имеет N + 1 ограниченную производную на отрезке [a, b]. Тогда погрешность интерполяционного многочлена Эрмита степени N выражается формулой

$ R_N (t) = \frac{{f^{(N + 1)} (\xi )}}{{(N + 1)!}}(t - t_0 )^{k_0 } (t - t_1)^{k_1 } \ldots (t - t_M)^{k_M}, $

где tn — интерполяционные узлы, n = 0, ..., M, ki - кратность i узла, \xi \in \left[{a, b}\right], N = k_0 + k_1 + \ldots + k_M - 1.

Поставим теперь следующую задачу: построить кусочно - кубическую интерполирующую функцию, непрерывную на отрезке [a, b] со своими двумя первыми производными.

Обозначим такую функцию S(t) ; значения производных в узлах tn обозначим mn = S'(tn). Если задать в узлах tn, tn + 1 значение функции и ее первой производной, то получим эрмитов кусочно - кубический полином

\begin{gather*} S(t) = \frac{{(t_{n + 1} - t)^2 \left[{2(t - t_n) + \tau }\right]}}{{\tau ^3 }}f_n + \frac{{(t - t_n)^2 \left[{2(t_{n + 1} - t) + \tau }\right]}}{{\tau ^3 }}f_{n + 1} + \\ + \frac{{(t_{n + 1} - t)^2 (t - t_n)}}{{\tau ^2 }}m_n + \frac{{(t - t_n)^2 (t - t_{n + 1})}} {{\tau ^2 }}m_{n + 1}, \end{gather*}

или

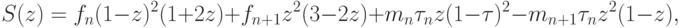
S(z) = f_{n}(1 - z)^{2}(1 + 2z) + f_{n + 1}z^{2}(3 - 2z) + m_{n}\tau _{n}z(1 - \tau )^{2} - m_{n + 1}\tau _{n}z^{2}(1 - z),

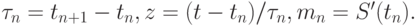
где \tau _{n} = t_{n + 1} - t_{n}, z = (t - t_{n})/\tau _{n}, m_{n} = S'(t_{n}).

6.9.1. Замечание о тригонометрической интерполяции

Для периодической функции f(t) с периодом T естественно строить приближение с использованием функций

$ \varphi_n(t) = a_n \cos {\frac{\pi nt}{T}} + b_n \sin{\frac{\pi nt}{T}} $
Тригонометрическая интерполяция состоит в замене f(t) тригонометрическим многочленом
$ F_N (t) = \sum\limits_{n = 0}^{N}{\varphi_n (t) = a_0 + \sum\limits_{n = 1}^{N}{(a_n \cos \frac{{\pi nt}}{T} + b_n \sin \frac{\pi nt}{T})}} $,
коэффициенты которого находятся при решении СЛАУ FN(tk) = f(tk), k = 1, ..., 2N + 1, t2N + 1 - t0 = T, здесь \left\{{t_k}\right\}_{k = 0}^{2N + 1} — последовательность узлов интерполяции.

Дальше >>
< Лекция 6 || Лекция 7: 1234567891011 || Лекция 8 >

Вопросы и ответы

вопросов: 1
Sanjar Ibrohimov
Sanjar Ibrohimov
ответить