Интерполяция функций
6.12. Интерполяция функций двух переменных
Пусть сетка образована пересечением прямых x = xn, n = 0, ..., N и y = ym, m = 0, ..., M, fnm = f(xn, ym) — значение функции в узле { xn, ym }. Воспользуемся, например, аппаратом кусочно - многочленной интерполяции. Для этого сначала реализуется кусочно - многочленная интерполяция заданной степени по x на каждой прямой y = ym. Затем при каждом значении x = xn реализуется кусочно - многочленная интерполяция по y с учетом значений функции, полученных на первом шаге. Так, в случае кусочно - линейной интерполяции по обоим переменным этот метод приводит (для случая прямоугольника ![x \in [x_n, x_{n + 1}], y \in [y_n, y_{n + 1}]](/sites/default/files/tex_cache/1cbb9efd1d5a9e0b42fcae6176a529a6.png) ) к интерполяционному многочлену
) к интерполяционному многочлену
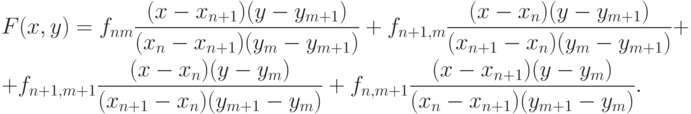
Сходным образом можно провести последовательную лагранжеву интерполяцию, но при каждом фиксированном значении m, затем — при каждом фиксированном значении n с учетом первого шага интерполяции. Общая формула такого интерполянта аналогична одномерной формуле для интерполяционного полинома в форме Лагранжа:
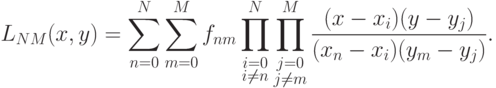
Если fA, fB, fD — значение функции f(x, y) в вершинах A, B, D, некоторого треугольника на треугольной расчетной сетке, то вычислить приближенное значение функции внутри этого треугольника можно с помощью билинейной функции  находя коэффициенты a, b, c из условий
находя коэффициенты a, b, c из условий
axA + byA + c = fA, axB + byB + c = fB, axD + byD + c = fD,
где {xA, yA}, {xB, yB}, {xD, yD} - координаты вершин A, B, D. Погрешность такой интерполяции для функции f(x, y) с непрерывными вторыми производными будет O(h2), где h — длина наибольшей стороны треугольника АВD.
6.13. Задачи
- Выписать интерполяционные полиномы первой и второй степени в форме Лагранжа и Ньютона.
Решение. Интерполяционные полиномы первой и второй степени в форме Лагранжа:

где t0, t1, t2 — узлы интерполяции, f(t1), f(t2), f(t3) - значения интерполируемой функции.
Интерполяционные полиномы первой и второй степени в форме Ньютона:
(t - t_2 ).
\end{gather*}](/sites/default/files/tex_cache/9aa13404b61b1f3efd4eb4b283ec1de8.png)
- Сравните количество арифметических действий, требуемое для вычисления интерполяционного
полинома, записанного в двух формах:
Ln(x) = a0 + a1t + ... + antn, Ln(x) = a0 + t(a1 + t(a2 + t(... (an - 1 + cnt) ...))) (схема Горнера)
Решение. В первом случае для вычисления значения в одной точке требуется
умножений и n сложений. Во втором — n умножений и n сложений.
- Задана система узлов интерполяции:

Какова погрешность интерполяции, если n = 3?
Решение. Сделаем замену переменных в выражении для остаточного члена
![$ R_3 (t) = (t - t_0)(t - \frac{t_0 + t_n}{2})(x - t_n), t = \frac{t_0 + t_n}{2} + \frac{t_n - t_0 }{2}z, z \in [- 1;1]. $](/sites/default/files/tex_cache/f045b9297fb9547d9e75180bbad96ec6.png)
Получим
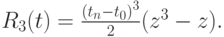
Полученный кубический полином имеет на [- 1;1] экстремумы в точках

В таком случае

- Предложите простой рекуррентный алгоритм вычисления коэффициентов
 интерполяционного полинома
интерполяционного полиномаPn(t) = a0 + a1(t - t0 ) + ... + an(t - t0) ... (t - tN - 1).
Решение. Для коэффициентов полинома получаем систему линейных уравнений с треугольной матрицей:
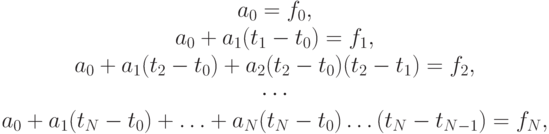
которая легко решается от первого уравнения к последнему:

- Оценить погрешность приближения функции ln t'(t' = 1, 23) при помощи интерполяционного полинома второй степени по точкам 1, 1; 1, 2; 1, 3.
Решение. Остаточный член интерполяции будет

при N = 2 имеем:
![\begin{gather*}
\varepsilon = \left|{f(x) - L_2 (t)}\right| \le \frac{{\max\limits_{[1, 1;1, 3]} \left|{f^{(3)} (t)}\right|}}{6}\left|{(t - t_0 )(t - t_1 )(t - t_2 )}\right|, \\
\max\limits_{[1, 3;1, 2]} \left|{f^{(3)} (t)}\right| = \frac{2}{{1 \cdot 1, 3}} \approx 1, 5.
\end{gather*}](/sites/default/files/tex_cache/397e698086419a29476063e134aa90b6.png)
В таком случае

- Показать, что погрешность интерполяции может быть выражена следующим образом:
f(t) - LN(t) = (t - t0) ... (t - tN)f(t, t0, ..., tN),
где f(t, t0, ..., tN) — разделенная разность порядка N.
Решение. Из выражения для разделенной разности порядка N + 1

получим выражение для f(t):

Тогда

Сравнивая полученное выражение с выражением для остаточного члена интерполяции
приходим к выводу, что для некоторой точки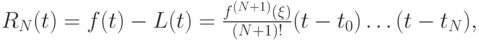
![\xi \in [t_0, t_N]](/sites/default/files/tex_cache/a813f09da70741c26ad206b86179afea.png) имеет место соотношение между разделенной разностью и производной порядка N + 1:
имеет место соотношение между разделенной разностью и производной порядка N + 1:
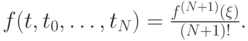
- Пусть значения функции f(t) заданы в узлах интерполяции t1, t2, t3. Построить функцию для которой выполнялось бы условие интерполяции: g(ti) = f(ti), i = 1, 2, 3 (задача дробно - линейной интерполяции ).

Решение. Из условий интерполяции
получаем систему трех линейных уравнений:
a0 + a1t1 - d0f1 = t1f1, a0 + a1t2 - d0f2 = t2f2, a0 + a1t3 - d0f2 = t3f3.
Вводя обозначения

и применив метод последовательного исключения неизвестных, получим
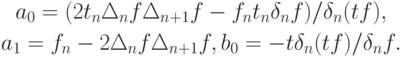
Здесь учтено, что
Разумеется, знаменатель дробно - рационального выражения не должен обращаться в нуль на рассматриваемом отрезке.
