НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 7: Интерполяция функций

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3791 / 1086 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 53 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

6.6. Интерполяционный полином в форме Ньютона

6.6.1. Разделенные и конечные разности

Определение. Пусть задана система узлов $\left\{{t_n}\right\}_{n = 0}^{N}, t_n \in \left[{a, b}\right], t_0 = a, t_N = b.$

Разделенные разности нулевого порядка в точке t_i совпадают со значениями функции f(t_i) ;

Разности первого порядка определяются для двух точек t_i, t_{i + 1} равенством

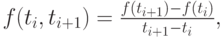
$f(t_i , t_{i + 1}) = \frac{{f(t_{i + 1}) - f(t_i)}}{{t_{i + 1} - t_i}},$

разности второго порядка — для трех точек t_i, t_{i + 1}, t_{i + 2}

$f(t_i , t_{i + 1}, t_{i + 2}) = \frac{f(t_{i + 1}, t_{i + 2}) - f(t_i , t_{i + 1})}{t_{i + 2} - t_i},$

разности порядка k — для k + 1 точки по рекуррентной формуле

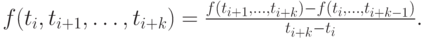
$f(t_i, t_{i + 1}, \ldots , t_{i + k}) = \frac{f(t_{i + 1}, \ldots , t_{i + k}) - f(t_i, \ldots , t_{i + k - 1})}{t_{i + k} - t_i}.$

Методом математической индукции можно показать, что

а)

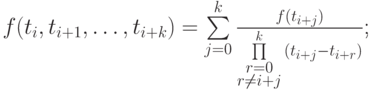
$$ f(t_i, t_{i + 1}, \ldots , t_{i + k}) = \sum\limits_{j = 0}^{k}{\frac{f(t_{i + j})}{\prod\limits_{\substack{r = 0 \\ r \ne {i + j}}}^{k}{(t_{i + j} - t_{i + r})}}} $;$

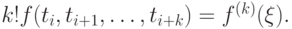
б) существует точка $\xi \in \left[{a, b}\right]$ такая, что $k!f(t_{i}, t_{i + 1}, …, t_{i + k}) = f^{(k)}(\xi ).$

Отсюда следует, что разделенная разность есть симметричная функция своих аргументов t_i, ..., t_{i + k} и она не изменяется при их перестановке.

Для удобства введем таблицу разделенных разностей:

t₀	f(t₀)			$\ldots$
		f(t₀, t₁)		$\ldots$
t₁	f(t₁)		f(t₀, t₁, t₂)	$\ldots$
		f(t₁, t₂)		$\ldots$
t₂	f(t₂)		$\ldots$	$\ldots$	f(t₀, …, t_n)
$\ldots$	$\ldots$	$\ldots$	f(t_{n - 2}, t_{n - 1}, t_n)	$\ldots$
		f(t_{n - 1}, t_n)		$\ldots$
t_n	f(t_n)			$\ldots$

Пусть сетка — равномерная. Тогда конечной разностью первого порядка функции f(t) в точке t_k с шагом $\tau$ называют величину $\Delta f_{k} = f_{k + 1} - f_{k},$ где f_k = f(t_k), второго порядка — величину

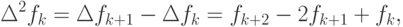
$\Delta ^{2}f_{k} = \Delta f_{k + 1} - \Delta f_{k} = f_{k + 2} - 2f_{k + 1} + f_{k},$

третьего

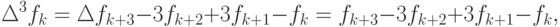
$\Delta ^{3}f_{k} = \Delta f_{k + 3} - 3f_{k + 2} + 3f_{k + 1} - f_{k} = f_{k + 3} - 3f_{k + 2} + 3f_{k + 1} - f_{k},$

четвертого

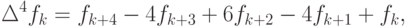
$\Delta ^{4}f_{k} = f_{k + 4} - 4f_{k + 3} + 6f_{k + 2} - 4f_{k + 1} + f_{k},$

причем

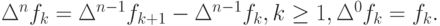
${\Delta}^{n} f_k = {\Delta}^{n - 1} f_{k + 1} - {\Delta}^{n - 1} f_k, k \ge 1, {\Delta}^0 f_k = f_k.$

Методом математической индукции доказывается формула

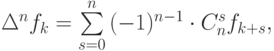
${\Delta}^{n} f_k = \sum\limits_{s = 0}^{n}{(- 1)^{n - 1} \cdot C_n^{s} f_{k + s}, }$

где $C_i^{s} = \frac{i!}{s!(i - s)!}$ - биномиальные коэффициенты.

Нетрудно показать, например, используя формулу Лагранжа, что существует точка $\xi \in \left[{a, b}\right]$ такая, что $\tau ^{n} f^{(n)} (\xi ) = {\Delta}^{n} f_k , t_k \in \left[{a, b}\right],$ поэтому в вычислительных методах используется приближенная формула

$f^{(n)} (t) \approx \frac{{\Delta}^{n} f_k}{\tau ^{n}},$

аналогичная тем формулам численного дифференцирования, что были получены в "Предмет вычислительной математики. Обусловленность задачи, устойчивость алгоритма, погрешности вычислений. Задача численного дифференцирования" методом неопределенных коэффициентов.

Заметим, что введенные конечные разности называют "разностями вперед". Аналогично можно ввести "разности назад":

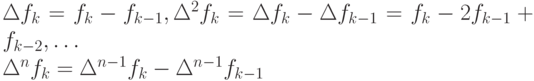
$\Delta f_{k} = f_{k} - f_{k - 1}, \Delta ^{2}f_{k} = \Delta f_{k} - \Delta f_{k - 1} = f_{k} - 2f_{k - 1} + f_{k - 2}, \dots \\ \Delta ^{n}f_{k} = \Delta ^{n - 1}f_{k} - \Delta ^{n - 1}f_{k - 1}$

и центральные разности

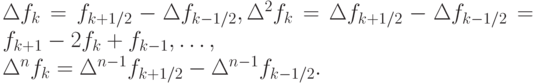
$\Delta f_{k} = f_{k + 1/2} - \Delta f_{k - 1/2}, \Delta ^{2}f_{k} = \Delta f_{k + 1/2} - \Delta f_{k - 1/2} = f_{k + 1} - 2f_{k} + f_{k - 1}, \dots , \\ \Delta ^{n}f_{k} = \Delta ^{n - 1}f_{k + 1/2} - \Delta ^{n - 1}f_{k - 1/2}.$

Иногда для обозначения первых конечных разностей вперед и назад используют обозначения 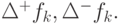$\Delta ^{+}f_{k}, \Delta ^{-}f_{k}.$

6.6.2. Интерполяционный полином в форме Ньютона

Интерполяционный полином может быть записан с использованием введенных выше разделенных разностей. Такая форма его записи называется интерполяционным полиномом в форме Ньютона. Полином имеет вид

N_n(t) = f(t₁) + f(t₁, t₂)(t - t₁) + ... + f(t₁, ..., t_{n + 1})(t - t₁) ... (t - t_n).

То, что это интерполяционный полином, может быть доказано, например, методом математической индукции. Отметим, что полином в форме Ньютона напоминает ряд Тейлора, а остаточный член интерполяционного полинома — остаточный член этого ряда. Достоинством записи интерполянта в форме Ньютона является то, что для повышения порядка полинома нет необходимости в его полной перестройке; достаточно лишь добавить к уже полученному выражению еще одно или несколько слагаемых. С помощью разделенных разностей можно оценивать погрешность интерполяции. Читатели могут предложить способ контроля точности вычислений, основанный на использовании разделенных разностей.

Дальше >>

Авторизоваться

Введение в вычислительную математику

Интерполяция функций

6.6. Интерполяционный полином в форме Ньютона

6.6.1. Разделенные и конечные разности

6.6.2. Интерполяционный полином в форме Ньютона

Вопросы и ответы