Приоритетные очереди

Операции с d-кучей

При реализации основных операций над кучами используются две вспомогательные операции — ВСПЛЫТИЕ и ПОГРУЖЕНИЕ. При реализации этих операций введем еще одну вспомогательную операцию — транспонирование, с помощью которой будем менять местами элементы, расположенные в двух разных узлах дерева. Ее реализация может быть представлена следующим образом:

Замечание. Если в кучу помещаются только ключи элементов, то процедура транспонирования модифицируется соответствующим образом.

Операция ВСПЛЫТИЕ.Эта операция применяется в тех случаях, когда в некотором узле, например в -м, расположен элемент , нарушающий кучеобразный порядок так, что его ключ меньше ключа его родителя .

Элементы и меняются местами. Если после этого элемент снова не удовлетворяет условиям кучи, то еще раз проводится аналогичная перестановка. И так до тех пор, пока не встанет на свое место.

Рассмотрим 3-дерево на рис. 4.3. В этом дереве кучеобразный порядок нарушает узел с ключом , так как его родительскому узлу приписан элемент с ключом .

Рис. 4.3.

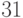Применим к узлу операцию ВСПЛЫТИЕ. Элементы с ключами и меняются местами. В результате получается дерево, представленное на рис. 4.4.

Рис. 4.4.

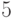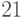Теперь нарушен кучеобразный порядок в узле ( ), меняем местами элементы c ключами и . В результате получаем кучу, изображенную на рис. 4.5. Кучеобразный порядок восстановлен, операция ВСПЛЫТИЕ завершена.

Рис. 4.5.

Вычислительная сложность этой операции пропорциональна числу сравнений элементов и их обменов. Это число, очевидно, не более чем удвоенное число узлов в пути от узла до корня дерева. Длина такого пути в -куче с узлами не превосходит ее высоты, а именно 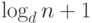, в соответствии с доказанным выше утверждением 1. Значит, время выполнения данной операции — .

Реализация операции ВСПЛЫТИЕ. Входным параметром этой операции является номер узла, в котором нарушен порядок:

Замечание.

1. Операцию ВСПЛЫТИЕ можно применять не только к -куче, но и к другим видам куч.
2. Для более эффективного выполнения операции ВСПЛЫТИЕ можно поступить следующим образом: запомнить элемент, находящийся в узле , переместить элемент из его родительского узла в узел , затем из узла 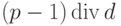в узел и так до тех пор, пока не освободится узел для запомненного элемента. После этого поместить запомненный элемент на освободившееся место. Более точно это можно выразить с помощью следующих операторов:

Операция ПОГРУЖЕНИЕ. Эта операция также применяется для восстановления свойства кучеобразности. Пусть, например, в -м узле расположен элемент , нарушающий кучеобразный порядок таким образом, что ключ элемента больше ключа элемента , приписанного потомку узла . В этом случае среди непосредственных потомков узла выбирается элемент с наименьшим ключом, и элементы и меняются местами. Если после этого элемент снова не удовлетворяет условиям кучи, то еще раз проводим аналогичную перестановку. И так до тех пор, пока не встанет на свое место.

Рассмотрим -дерево, представленное на рис. 4.6. В узле расположен элемент с ключом 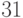, и этот узел имеет двух потомков с меньшими ключами, а именно и . Применим к элементу операцию ПОГРУЖЕНИЕ.

Рис. 4.6.