НОУ ИНТУИТ | Лекция | Приоритетные очереди

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 26.09.2006 | Доступ: свободный | Студентов: 1740 / 445 | Оценка: 4.25 / 4.12 | Длительность: 17:09:00

ISBN: 978-5-9556-0066-6

Тема: Алгоритмы и дискретные структуры

Специальности: Программист, Математик

|

Вам нравится? Нравится 19 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Операция УМЕНЬШЕНИЕ_КЛЮЧА. Предназначена для уменьшения ключа у элемента, приписанного узлу с заданным номером , на заданную величину $\Dl$ . Это действие может нарушить кучеобразный порядок лишь таким образом, что уменьшенный ключ элемента в узле станет меньше ключа элемента в родительском узле. Для восстановления порядка в куче используется операция ВСПЛЫТИЕ.

Вычислительная сложность данной операции определяется временем, затрачиваемым на уменьшение ключа (то есть константой), и временем выполнения операции ВСПЛЫТИЕ (то есть $O(\log_d n))$ . В итоге вычислительная сложность операции УМЕНЬШИТЬ_КЛЮЧ равна $O(\log_d n)$ .

Реализация операции УМЕНЬШЕНИЕ_КЛЮЧА

$\formula{ \t{procedure УМЕНЬШИТЬ\_КЛЮЧ}\ (i, delta);\\ \t begin\ {\rm key}[{i}] := {\rm key}[{i}] - {delta};\ \t{ВСПЛЫТИЕ}\ (i);\ \t end; }$

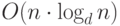Операция ОКУЧИВАНИЕ. Заметим, что если -куча создается путем -кратного применения операции ВСТАВКА, то суммарная трудоемкость ее создания будет равна $O(n\cdot \log_d n)$ . 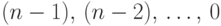Если же все элементов сначала занимают в произвольном порядке массив $a[0 \ldots (n - 1)]$ и, соответственно, массив ${\rm key}[0 \ldots ({n} - 1)]$ , то можно превратить их в -кучу, применяя операцию ПОГРУЖЕНИЕ по очереди к узлам $(n - 1),\,(n - 2),\,\ldots,\,0$ .

Такой процесс будем называть окучиванием массива. Для доказательства того, что в результате действительно устанавливается кучеобразный порядок, достаточно заметить, что если поддеревья с корнями в узлах 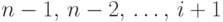$n - 1,\, n - 2,\, \ldots,\, i + 1$ упорядочены по правилу кучи, то после применения процедуры ПОГРУЖЕНИЕ к узлу поддерево с корнем в этом узле также станет упорядоченным по правилу кучи. Итак, остановимся на следующей реализации.

Реализация операции ОКУЧИВАНИЕ

$\formula{ \t{procedure ОКУЧИВАНИЕ};\\ \t begin\\ \mbox{}\q \t for\ i:= n - 1\ \t downto\ 0\ \t do\ \t{ПОГРУЖЕНИЕ}\ (i)\\ \t end; }$

Утверждение 3. Вычислительная сложность операции ОКУЧИВАНИЕ равна O(n) .

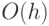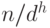Доказательство Заметим, что трудоемкость погружения с высоты равна O(h) , а количество узлов высоты не превосходит n/d^h . Осталось оценить сумму

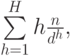
$\eq*{ \suml_{h=1}^{H} h\frac{n}{d^{h}}, }$

где $H = \lceil \log_d n\rceil$ , и убедиться, что полученная сумма есть O(n)

.

Для суммирования можно воспользоваться формулой

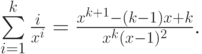
$\eq*{ \suml_{i=1}^k \frac{i}{x^i} = \frac{x^{k+1} - (k-1) x + k}{x^k (x-1)^2}. }$

Предоставляем читателю возможность завершить доказательство.

Операция СОЗДАТЬ_СПИСОК_МИНИМАЛЬНЫХ. Эта операция применяется для получения списка элементов, которые имеют ключи, меньшие заданного значения ${\rm key}0$ , и реализуется следующим образом. Если ключ элемента, находящегося в корне, больше, чем ${\rm key}0$ , то это дерево не имеет искомых элементов. В противном случае включаем его в выходной список , а затем применяем ту же процедуру ко всем потомкам узла, включенного в список.

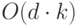Пусть куча содержит элементов с ключами, меньшими, чем ${\rm key}0$ . По свойству кучи, они все расположены на ее "верхушке". Данная процедура обходит эту верхушку за время, пропорциональное , и для каждого из этих элементов просматривает все его (или меньше) непосредственных потомков. Получаем, что время выполнения данной процедуры является величиной $O(d\cdot k)$ .

Реализация операции СОЗДАТЬ_СПИСОК_МИНИМАЛЬНЫХ

$\formula{ \t{procedure СОЗДАТЬ\_СПИСОК\_МИНИМАЛЬНЫХ}(S, {\rm key}0);\\ \t begin\\ \mbox{}\q \t{Инициализируем пустой список} S; \\ \mbox{}\q \t{Инициализируем стек};\\ \mbox{}\q 0 \Rightarrow \t{стек};\\ \mbox{}\q \t{ while стек не пуст do}\\ \mbox{}\q\qq \t{begin стек} \Rightarrow i;\\ \mbox{}\q\qq\qq if ({\rm key}[i] < {\rm key}0)\ \t{then Добавить} a[i]\ \t{к списку}\ S;\\ \mbox{}\q\qq\qq \t for\ j:=d^\ast i + 1\ \t to\ d^\ast(i + 1)\ \t do if\ j \le (n - 1)\ \t then\ j \Rightarrow \t{стек};\\ \mbox{}\q\qq \t end\\ \t end }$

Сводные данные о трудоемкости операций с d-кучами

ВСПЛЫТИЕ	$O(\log_d n)$
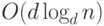ПОГРУЖЕНИЕ	$O(d \log_d n)$
ВСТАВКА 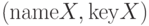$({\rm name}X, {\rm key}X)$	$O(\log_d n)$
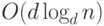УДАЛЕНИЕ	$O(d \log_d n)$
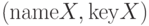
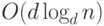УДАЛЕНИЕ_МИН $({\rm name}X, {\rm key}X)$	$O(d \log_d n)$
MINKEY
УМЕНЬШЕНИЕ_КЛЮЧА	$O(\log_d n)$
ОБРАЗОВАTЬ_ОЧЕРЕДЬ
СПИСОК_МИН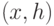

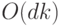Замечание. Для -куч "неудобной" является операция слияния куч.

Применение приоритетных очередей в задаче сортировки

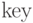Под задачей сортировки в простейшем случае понимают следующее: дана последовательность $({\rm key}[1],\,{\rm key}[2],\, \ldots,\, {\rm key}[{n}])$ из элементов некоторого линейно упорядоченного множества, например целых или вещественных чисел, записанных в массив ${\rm key}$ . Требуется переставить элементы массива так, чтобы после перестановки выполнялись неравенства:

$\eq*{ {\rm key}[1] \le {\rm key}[2] \le \ldots \le {\rm key} [n]. }$

Уточнения этой задачи связаны с теми средствами, с помощью которых предполагается ее решение. Нас интересуют алгоритмы с точки зрения их компьютерной реализации. Оценивая качество различных алгоритмов, обычно интересуются тем, как зависит время счета от длины сортируемой последовательности и требуется ли для этого дополнительная память, размер которой определяется параметром . Существенную роль при этом играет метод доступа к элементам памяти. При сортировке во внутренней (оперативной) памяти обычно используется прямой доступ, а во внешней — последовательный.

Дальше >>

Структуры данных и модели вычислений

Приоритетные очереди

Применение приоритетных очередей в задаче сортировки

Вопросы и ответы

Авторизоваться

Структуры данных и модели вычислений

Приоритетные очереди

Применение приоритетных очередей в задаче сортировки

Вопросы и ответы