НОУ ИНТУИТ | Структуры данных и модели вычислений. Лекция 4: Приоритетные очереди

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 26.09.2006 | Доступ: свободный | Студентов: 1800 / 485 | Оценка: 4.25 / 4.12 | Длительность: 17:09:00

ISBN: 978-5-9556-0066-6

Тема: Алгоритмы и дискретные структуры

Специальности: Программист, Математик

|

Вам нравится? Нравится 19 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Среди непосредственных потомков узла 1 находим узел, которому приписан элемент с наименьшим ключом, в нашем случае это узел 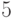c ключом . Меняем местами элементы и . В результате получается дерево, изображенное на рис. 4.7.

Рис. 4.7.

Теперь элемент снова имеет потомка с меньшим, чем у него, ключом (а точнее, оба его потомка имеют меньшие ключи). Снова находим непосредственного потомка элемента с наименьшим ключом, и меняем его и местами. Получается дерево, изображенное на рис. 4.8.

Рис. 4.8.

Теперь находится в узле 17 и не имеет потомков с меньшим, чем у него, ключом (точнее, у него вообще нет потомков). Операция ПОГРУЖЕНИЕ завершена.

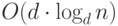Вычислительная сложность этой операции пропорциональна числу сравнений элементов и их обменов. Для каждого узла в пути следования данной операции производится сравнений (при поиске потомка с минимальным ключом) и один обмен. Длина этого пути в -куче с узлами не превосходит ее высоты, а именно $\log_d n$ , по доказанному выше утверждению 1. Значит, время выполнения данной операции — $O(d\cdot \log_d n)$ .

Для реализации операции погружения воспользуемся функцией ${\rm minchild} (i)$ , позволяющей для любого узла находить его непосредственного потомка с минимальным ключом. Если у узла нет потомков, то ${\rm minchild} (i) = 0$ .

Реализация операции ПОГРУЖЕНИЕ

$\formula{ \t{procedure ПОГРУЖЕНИЕ}(i);\\ \t begin \\ \mbox{}\q c:= {\rm minchild}(i);\\ \mbox{}\q \t while\ (c \ne 0)\ \t and\ ({\rm key}[c] < {\rm key}[i])\ \t do\ \{{\rm tr}(i, c);\ i:= c;\ c := {\rm minchild} (c)\}\\ \t end; }$

$\formula{ \t function\ {\rm minchild} (i);\\ \t begin\ \t if\ i\cdot d + 1 > n\ \t then\ {\rm minchild} := 0\ \t else\\ \mbox{}\q \t begin\\ \mbox{}\q\qq {\rm first\_child}:= i\cdot d + 1;\ {\rm last\_child}:= \min((i + 1)\cdot d - 1, n);\\ \mbox{}\q\qq{\rm min\_key} := {\rm key}[{\rm first\_child}];\\ \mbox{}\q\qq \t for\ i := {\rm first\_child}\ \t to\ {\rm last\_child}\ \t do\ \t if\ {\rm key}[i] > {\rm min\_key}\ \t then\\ \mbox{}\q\qq\qq \{{\rm min\_key} := {\rm key}[i];\ {\rm minchild} := i\}\\ \mbox{}\q \t end\\ \t end }$

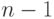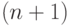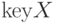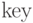Операция ВСТАВКА. Если перед выполнением этой операции куча содержала узлов (напомним, что они пронумерованы числами от до {n - 1} ), то добавляем к дереву (n + 1) -й узел (его номер будет ) и приписываем ему элемент с именем ${\rm name}X$ и ключом ${\rm key}X$ . Вставка нового элемента производится посредством отведения для него места в -ых позициях массивов и ${\rm key}$ соответственно, после чего к добавленному узлу применяется операция ВСПЛЫТИЕ для восстановления кучеобразного порядка.

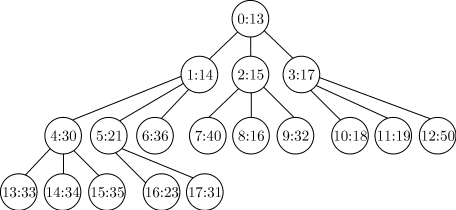
Вставим в -кучу, изображенную на рис. 4.9, новый элемент с ключом .

Рис. 4.9.

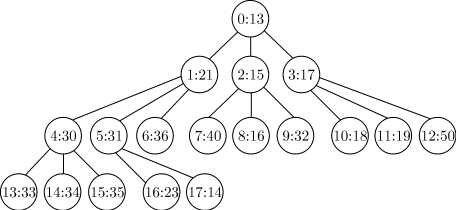
Сначала добавляем к дереву новый узел с номером и приписываем ему элемент с ключом . Получим дерево, представленное на рис. 4.10.

Рис. 4.10.

Затем применяем к узлу операцию ВСПЛЫТИЕ. При описании этой операции использовался именно приведенный пример (см. рис. 4.3, 4.4, 4.5).

Вычислительная сложность данной операции равна константе плюс вычислительная сложность операции ВСПЛЫТИЕ, то есть $O(\log_d n)$ .

Реализация операции ВСТАВКА

$\formula{ \t{procedure ВСТАВКА}\ ({\rm name}X, {\rm key}X);\\ \t begin\ {a}[{n}]:= {\rm name}X; {\rm key}[{n}]:= {\rm key}X;\ \t{ВСПЛЫТИЕ}\ ({n});\ {n}:= {n} + 1\ \t end; }$

Операция УДАЛЕНИЕ. Используется для удаления элемента, приписанного узлу с заданным номером . Сначала элемент, приписанный последнему узлу дерева, переносится на место удаляемого элемента, последний узел при этом становится ненужным и поэтому удаляется из дерева. Далее, если узел , в который помещен новый элемент, имеет родителя с большим ключом, то к узлу применяется операция ВСПЛЫТИЕ, в противном случае — ПОГРУЖЕНИЕ.

Таким образом, ориентируясь на худший случай, вычислительную сложность операции УДАЛЕНИЕ оцениваем величиной 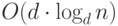$O(d\cdot \log_d n)$ .

Реализация операции УДАЛЕНИЕ

$\formula{ \t{procedure УДАЛЕНИЕ}(i);\\ \t begin\ {a}[{i}]:= {a}[{n} - 1];\ {\rm key}[{i}]:= {\rm key}[{n} - 1];\ {n}:= {n} - 1; \\ \mbox{}\q \t if\ i \ne 0\ \t and\ {\rm key}[{i}] ({\rm key}[(i - 1) \mathop{\rm div} {d}]\ \t then\ \t{ВСПЛЫТИЕ}({i})\\ \mbox{}\q \t else\ \t{ПОГРУЖЕНИЕ}({i})\\ \t end; }$

Операция УДАЛЕНИЕ_МИНИМУМА. Эта операция предназначена для взятия из кучи элемента с минимальным ключом (он находится в корне дерева) и удаления его из кучи с помощью операции УДАЛЕНИЕ.

Реализация операции УДАЛЕНИЕ_МИНИМУМА

$\formula{ \t{procedure УДАЛЕНИЕ\_МИНИМУМА}\ ({\rm name}X, {\rm key}X);\\ \t begin\ {\rm name}X:= {a}[0];\ {\rm key}X:= {\rm key}[0];\ \t{УДАЛЕНИЕ}\ (0)\ \t end; }$

Функция MINKEY. Эта функция предназначена для определения минимального ключа без удаления соответствующего элемента.

Реализация функции MINKEY

$\formula{ \t function\ {\rm MINKEY};\ \t begin\ {\rm MINKEY}: = {\rm key}[0]\ \t end; }$

Трудоемкость операции, очевидно, равна {O}(1) .

Дальше >>

Авторизоваться

Структуры данных и модели вычислений

Приоритетные очереди

Вопросы и ответы