| Россия |
Инспектор
Вы можете этот курс.
Опубликован: 25.10.2007 | Уровень: профессионал | Доступ: платный
Лекция 7:
Понятие о методах конечных элементов
Примеры согласованных базисных функций. Если используется базис из "крышечек", то в каждом узле (при стыковке конечных элементов) решение МКЭ будет иметь разрыв первой производной. Это происходит из - за выбора базиса МКЭ. Сама искомая функция непрерывна.
Допустим, необходимо найти решение, обладающее непрерывной первой производной.
Строим набор функций базиса:
Считаем, что размер конечного элемента равен 1. Для одномерной сетки всегда найдется линейное преобразование (свое для каждого элемента!), переводящее данный элемент в отрезок длины 1. Положим, что базисная функция есть
![\varphi_i (x) \equiv 0, \mbox{ если } x \notin [- 1;1],](/sites/default/files/tex_cache/caa94984022146b1fc93cd120c7315f5.png)
а на каждом отрезке [- 1;0] , [0;1] — полином степени p. В точках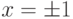 
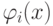и все ее производные до порядка m - 1 равны нулю. В точке x = 0
(в случае равномерного разбиения отрезка на конечные элементы). Тогда 
j = 0, ..., N; i = 1, ..., m - базис.
Рассмотрим случай 
. Тогда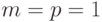 
, на каждом
отрезке функция линейна. Приходим к набору из "крышечек".
Возьмем p = 3, тогда m = 2. Строим набор базисных функций.
Фиксируем i = 1. На отрезках [- 1;0], [0;1] получаем полином степени 3.
![\varphi_1 (x) = a_0 + a_1 x + a_2 x^2 + a_3 x^3 (\mbox{на} [- 1;0]).](/sites/default/files/tex_cache/e0b8f08a5d7a56920ada303bd869c108.png)
Условия: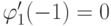 
, 
, 
, 
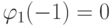определяют коэффициенты
a0 = 1; a1 = 0; a2 = - 3; a3 = - 2.
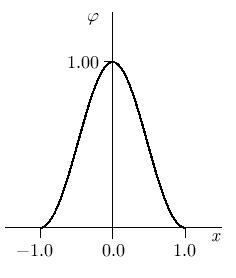
В итоге на отрезке [- 1;0]
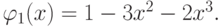
Аналогично поступаем на отрезке [0;1], там имеем
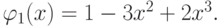
График базисной функции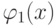 
представлен на рис. 7.9.
Пусть теперь i = m = 2. Строим набор 
такой, что
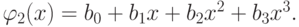
Из условий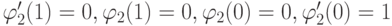 
получается
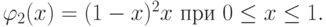
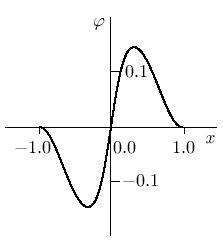
Аналогично,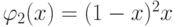 
при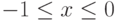 
. График функции изображен на рис.
7.10.
Базис является согласованным, если для уравнения степени не выше p + 1 все базисные функции непрерывны (принадлежат Cm ).
Что представляет собой метод Галеркина при использовании такого базиса? Теперь в точках сетки (межэлементных) необходимо знать не только функцию u, но и ее первую, вторую, ..., (m - 1) - ю производную по x:
![\begin{gather*}
u^{h} = \sum\limits_{j = 1}^{N}{[u(a + jh) \varphi_{1j}^{h} (x) + u^{\prime}_x (a + jh) \varphi_{2j}^{h} (x)]}, \\
u^{h} = \sum\limits_{j = 1}^{N}{(c_j \psi_{1j}^{N} + b_j \varphi_{2j}^{N} (x)]}.
\end{gather*}](/sites/default/files/tex_cache/cda9c841966307eda70ec2590efa32ae.png)
Отметим, что u(a + jh) и u'x(a + jh) определяются численно при решении уравнений методом Галеркина.
Увеличилось число базисных функций и коэффициентов разложения.
Заметим также, что матрица системы — разреженная, но уже не трехдиагональная (если порядок системы выше второго).
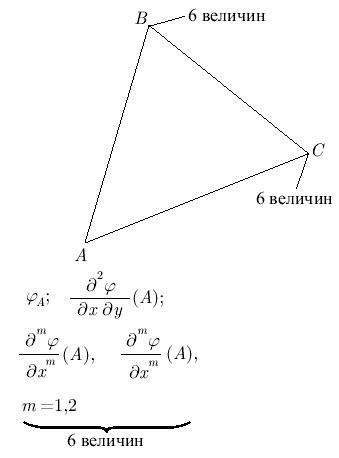
Согласование в двумерном случае. Надо сшивать следующие величины (рис. 7.11): 18 величин в узлах плюс 
значения нормальных производных на гранях.
Получается 21 условие, значит необходимо иметь 21 произвольную константу. Полином должен иметь достаточно высокую степень (члены до x5, y5 ). Поэтому в многомерном случае, как правило, используются несогласованные базисные функции или с низким (m = 1) порядком согласования.
