Численные методы решения уравнений в частных производных

:

Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Уровень: профессионал | Доступ: платный
Лекция 7:

Понятие о методах конечных элементов
A
|
версия для печати
< Лекция 6 || Лекция 7: 12345678 || Лекция 8 >

7.4. Пример построения схемы конечных элементов

Для уменьшения числа выкладок считаем, что

h_i = h_{i + 1} \equiv h \quad \mbox{для всех} \quad i (h_i \equiv x_i - x_{i - 1}).

Рассмотрим несамосопряженный аналог задачи (7.1):

\begin{gather*} - k(x)u^{\prime\prime}_x + q(x)u^{\prime}_x + p(x)u(x) = f(x), \\ u(0) = a; \quad u(1) = b; \\ k(x) \ge k_0 > 0; \quad p(x) \ge 0. \end{gather*}

Найдем сопряженное уравнение:

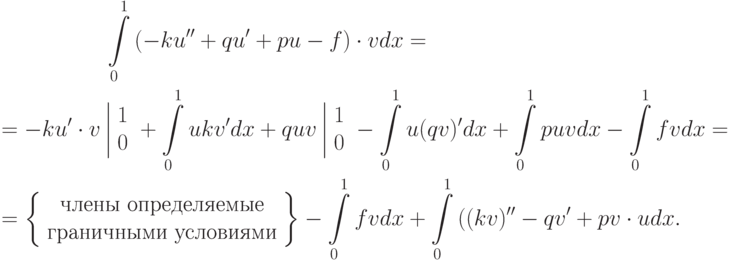
\begin{gather*} \int\limits_0^1 {(- ku^{\prime\prime} + qu^{\prime} + pu - f) \cdot vdx} = \\ = - ku^{\prime} \cdot v \left|\begin{array}{l} 1 \\ 0 \\ \end{array}\right. + \int\limits_0^1 {ukv^{\prime}dx} + quv \left|\begin{array}{l} 1 \\ 0 \\ \end{array}\right. - \int\limits_0^1 {u(qv) ^{\prime}dx} + \int\limits_0^1 {puvdx} - \int\limits_0^1 {fvdx} = \\ = \left\{\begin{array}{c} {\mbox{члены определяемые}} \\ {\mbox{граничными условиями}} \\ \end{array}\right\} - \int\limits_0^1 {fvdx} + \int\limits_0^1 {((kv) ^{\prime\prime} - qv^{\prime} + pv \cdot udx}. \end{gather*}

Из этого соотношения легко получить условия, при которых 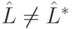\hat{L} \ne \hat{L}^*. Теперь запишем разложение по базису:

u^{N} = \psi_0^{N} + \sum\limits_{j = 1}^{N}{C_j \psi_j^{N}}

подставляем в исходное дифференциальное уравнение:

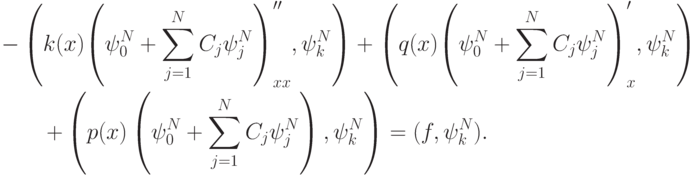
\begin{gather*} - \left(k(x) {\left(\psi_0^{N} + \sum\limits_{j = 1}^{N} C_j \psi_j^{N}\right)}^{\prime\prime}_{xx}, \psi_k^{N}\right) + \left(q(x) {\left(\psi_0^{N} + \sum\limits_{j = 1}^{N}C_j \psi_j^{N}\right)}^{\prime}_x, \psi_k^{N}\right) \\ + \left({p(x) \left({\psi_0^{N} + \sum\limits_{j = 1}^{N}{C_j \psi_j^{N}} }\right), \psi_k^{N}}\right) = (f, \psi_k^{N}). \end{gather*}

Рассмотрим отдельно каждое слагаемое в левой части:

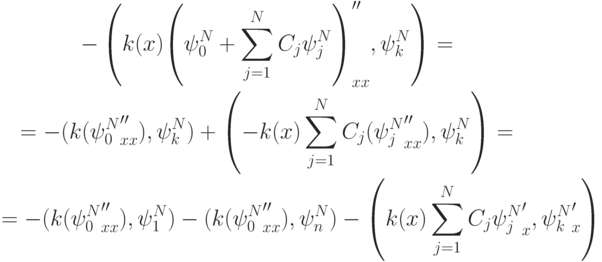\begin{gather*} - \left(k(x) {\left(\psi_0^{N} + \sum\limits_{j = 1}^{N}C_j \psi_j^{N}\right)}^{\prime\prime}_{xx}, \psi_k^{N}\right) = \\ = - (k({\psi_0^{N}}_{xx}^{\prime\prime}), \psi_k^{N}) + \left(- k(x) \sum\limits_{j = 1}^{N} C_j({\psi_j^{N}}^{\prime\prime}_{xx}), \psi_k^{N}\right) = \\ = - (k({\psi_0^{N}}_{xx}^{\prime\prime}), \psi_1^{N}) - (k({\psi_0^{N}}_{xx}^{\prime\prime}), \psi_n^{N}) - \left(k(x) \sum\limits_{j = 1}^{N} C_j {\psi_j^{N}}^{\prime}_x , {\psi_k^{N}}^{\prime}_x \right) \end{gather*} ( 7.11)

Первые два слагаемые в правой части получаются в силу того, что носители базисных функций финитны. Последнее слагаемое в правой части получается интегрированием по частям. Зачем необходимо интегрирование по частям? На первый взгляд ({\Psi^{N}_j})_{xx}^{\prime\prime} = 0. Но эта производная базисной функции — обобщенная функция, следовательно, в скалярных произведениях появятся \delta - функции, при интегрировании возникнут сложности.

В итоге после всех необходимых вычислений коэффициент перед Ck

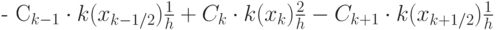
- C_{k - 1} \cdot k(x_{k - 1/2}) \frac{1}{h} + C_k \cdot k(x_k ) \frac{2}{h} - C_{k + 1} \cdot k(x_{k + 1/2}) \frac{1}{h}

Функция k(x) считается кусочно - постоянной на соответствующих отрезках, можно использовать какую - либо другую аппроксимацию (k \varphi_j^{N})_x ^{\prime} , учитывая что k(x) — заданная функция.

Первые два слагаемые в правой части (7.11) зависят от граничных условий и относятся к правой части системы уравнений для определения Ck.

Рассмотрим теперь

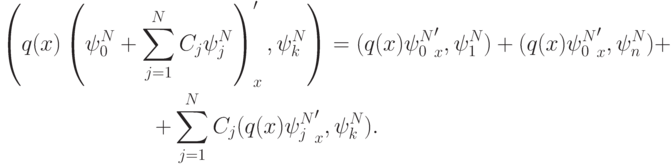
\begin{gather*} \left({q(x) \left({\psi_0^{N} + \sum\limits_{j = 1}^{N} {C_j \psi_j^{N}} }\right)^{\prime}_x , \psi_k^{N}}\right) = (q(x) {\psi_0^{N}}_x ^{\prime}, \psi_1^{N}) + (q(x){\psi_0^{N}}_x^{\prime}, \psi_n^{N}) + \\ + \sum\limits_{j = 1}^{N}{C_j (q(x){\psi_j^{N}}_x ^{\prime}, \psi_k^{N})}. \end{gather*}

Коэффициенты при Ck будут следующие:

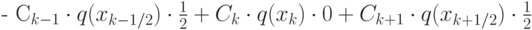
- C_{k - 1} \cdot q(x_{k - 1/2}) \cdot \frac{1}{2} + C_k \cdot q(x_k ) \cdot 0 + C_{k + 1} \cdot q(x_{k + 1/2}) \cdot \frac{1}{2}

Здесь опять предполагается, что функция q(x) кусочно - постоянная.

Последнее слагаемое с p(x) дает выражение

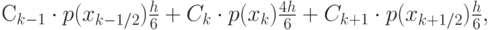
C_{k - 1} \cdot p(x_{k - 1/2}) \frac{h}{6} + C_k \cdot p(x_k) \frac{{4h}}{6} + C_{k + 1} \cdot p(x_{k + 1/2}) \frac{h}{6},

т.е. при "плохом" способе вычисляемых интегралов фактически получаем конечно - разностное соотношение, похожее на аппроксимацию Нумерова.

Вместе с тем, существует значительное отличие. Сеточная функция — это функция, заданная таблично. Решение (приближенное) МКЭ — это не сеточная функция, а элемент 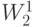W_2^1.

Дальше >>
< Лекция 6 || Лекция 7: 12345678 || Лекция 8 >

Вопросы и ответы

вопросов: 0

Студенты

всего: 30
Максим Радунцев
Максим Радунцев
Россия
предложить дружбу
Надежда Павленко
Надежда Павленко
Россия, Ставрополь
предложить дружбу