| Россия |
Инспектор
Вы можете этот курс.
Опубликован: 25.10.2007 | Уровень: профессионал | Доступ: платный
Лекция 7:
Понятие о методах конечных элементов
7.3. Формулировка проекционного метода Галеркина
По - прежнему рассматриваем задачи (7.1) и (7.2).
В дальнейшем будет рассмотрен класс дифференциальных операторов. Главный
недостаток метода Ритца — применимость лишь к дифференциальным задачам,
допускающим вариационную формулировку, т.е. в линейном случае 
— самосопряженный положительно определенный оператор (все собственные числа положительны).
Наряду с формулировкой (7.1) и (7.2) будем использовать запись, определяющую слабое (обобщенное) решение:
 |
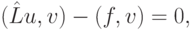( 7.8) |
где v — любая функция из рассмотренного ранее
функционального пространства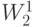 
, а скалярное произведение определено как
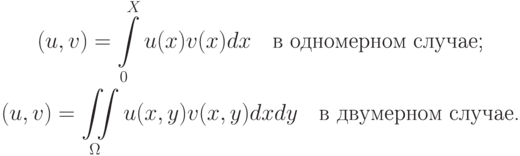
Равенство (7.8) определяет обобщенное решение задачи. Известно, что если u — классическое решение задачи, то оно является обобщенным
решением в смысле (7.8). Обратное, по понятным причинам, неверно — в 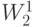"больше" функций, чем в C1 или C2. У задачи может существовать обобщенное решение, но не существовать классического.
Рассмотрим конечномерное подпространство пространства 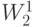с
введенным базисом:
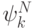— базисные функции в 
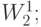они обязаны обладать теми же свойствами, что и базисные функции для метода Ритца. Рассмотрим теперь для (7.8) конечную систему весовых функций из : 
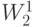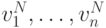. Вместо (7.8) рассмотрим конечную систему проекций на весовые функции.
Введем также обозначение
 |
( 7.9) |
здесь R — невязка. Тогда, после подстановки разложения по базисным функциям в (7.8), получим систему соотношений
 |
( 7.10) |
Минимум невязки в пространстве, определяемом функциями 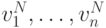достигается тогда, когда невязка принадлежит его ортогональному дополнению: 
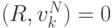для всех k. Теперь
надо потребовать, чтобы весовые функции образовывали базис в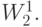 
Естественно в качестве весовых функций использовать уже имеющиеся базисные 
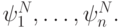Тогда получаем проекционный метод Галеркина.
В итоге для определения коэффициентов разложения по базису из конечных элементов имеем систему соотношений вида
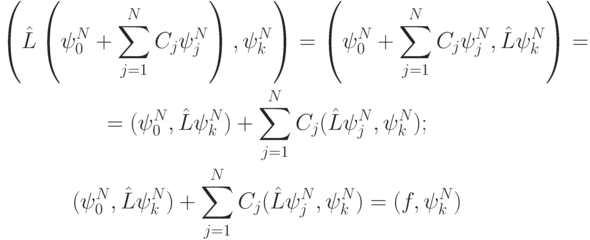
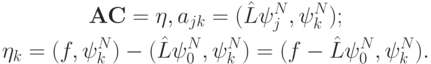
Это же соотношение получается и при выводе системы уравнений для коэффициентов в методе Ритца.
При вычислении скалярных произведений использовалась самосопряженность
линейного дифференциального оператора 
Но при выводе соотношения (7.10) самосопряженность оператора не использовалась! Значит, метод Галеркина можно обобщать и на случай несамосопряженного (и нелинейного!) дифференциального оператора. При использовании в качестве базисных функций "функций - крышечек", введенных выше, получаем вариант МКЭ. Для задач (7.1) и (7.2) метод будет давать те же соотношения, что и метод Ритца.
