НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 7: Понятие о методах конечных элементов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать программу

7.5. Построение базисных функций

Математическая основа МКЭ — метод Галеркина и вариационный метод Ритца — развиваются, начиная со второго десятилетия XX века. Прогресс в МКЭ последних лет заключается именно в построении наборов базисных функций, обладающих достаточной гладкостью — так называемых согласованных базисов.

Базис из "крышечек" в двумерном случае. Процесс построения базисных функции включает в себя:

триангуляцию области — разбиение на треугольники, каждый из которых является носителем своей базисной функции ;
построение базисных функций.

Требования к триангуляции (обозначения на рис. 7.3).

Рис. 7.3.

Между точками S и S^h с помощью нормалей к S устанавливается взаимно - однозначное соответствие, расстояние между соответствующими точками не превосходит $\delta_1 h^2$ ( h — сеточный параметр).
Длины сторон треугольников и их площади лежат в пределах [hl₁, hl₂] и $[h^{2}\gamma _{1} , h^{2}\gamma _{2}]$ , где $l_{1}, l_{2}, \gamma _{1}, \gamma _{2}$ — положительные константы, не зависящие от h.
Существует непрерывное взаимно - однозначное преобразование D^h на область, границы которой параллельны осям координат, или составляют с ними угол $\pi /4.$ Преобразование линейно внутри каждого треугольника и переводит последний в равнобедренный прямоугольный треугольник с катетами, равными h.

Простейший пример построения триангуляции.

Область D вписываем в прямоугольник.
Строим в прямоугольнике равномерную сетку с шагом h (рис. 7.4).

Рис. 7.4.
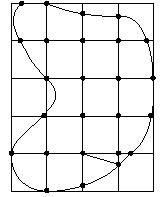
Ближайшие к границе D узлы сетки сдвигаем на границу D (рис. 7.5).

Рис. 7.5.
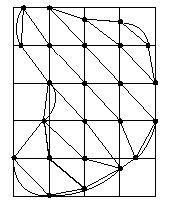
Разбиваем четырехугольники внутри D^h диагоналями (рис. 7.6).

Рис. 7.6.
Убираем все ячейки, пересечение которых с D^h пусто (рис. 7.7).

Рис. 7.7.

Рис. 7.8.

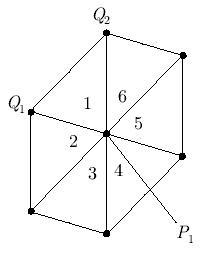
Построение базисной функции — "крышечки". Фиксируем вершину P₁ какого - либо треугольника. Составляем список соседей — вершин, принадлежащих треугольникам, имеющим вершину P₁. Пусть в списке есть вершины Q₁ и Q₂, принадлежащие треугольнику 1 (рис. 7.8). В этом треугольнике представляем

$\varphi_1 (x, y) = \frac{{1 - \frac{{y - y_1}}{{y_2 - y_1}} - \frac{{x - y_2}}{{x_1 - y_2}}}}{{1 - \frac{{y_{P_1} - y_1}}{{y_2 - y_1}} - \frac{{x_{P_1} - y_2}}{{x_1 - y_2}}}}.$

Тогда для точки

$P_1 \psi_{P_1}^{N} (x, y) = \sum\limits_{k = 1}^6 {\varphi_k (x, y)}.$

К сожалению, базисных функций типа "крышечек" может не хватить для решения уравнений второго (по пространственной производной) порядка. До сих пор рассматривались уравнения второго порядка. Перейдем теперь к модельному уравнению

${\frac{{d^4 u}}{{dx^4 }} + au = f(x); x \in [0, X]}$

( 7.12)

с какими - либо граничными условиями.

Будем искать решение в соответствии с методами МКЭ:

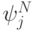${u^{N} = \psi_0^{N} + \sum\limits_{j = 1}^{N} {C_j \psi_j^{N}}, }$

( 7.13)

где $\psi_j^{N}$ обладают финитным носителем. Подставляем разложение (7.13) в (7.12). Отвлекаясь от членов с граничными условиями, отнесенными к $\psi_0^{N}$ , при умножении на $\psi_{l}^{N}$ имеем

$\begin{gather*} \left({\frac{d^4}{dx^4} \sum\limits_{j = 1}^{N}{C_j \psi_j^{N}}, \psi_{l}^{N}}\right) = \int\limits_0^{X}{\sum\limits_{j = 1}^{N}{C_j \frac{d^4 \psi_j^{N}}{dx^4} \psi_{l}^{N}} dx} = \\ = \int\limits_0^{X}{\sum\limits_{j = 1}^{N}{C_j \frac{d^2 \psi_j^{N}}{dx^2} \frac{d^2 \psi_{l}^{N}}{dx^2}} dx} = \left({\sum\limits_{j = 1}^{N}{C_j \frac{d^2 \psi_j^{N}}{dx^2}}, \frac{d^2 \psi_{l}^{N}}{dx^2}} \right) \times \\ \times {\left({\sum\limits_{j = 1}^{N}{C_j \frac{d^2 \psi_j^{N}}{dx^2}}, \frac{d^2 \psi_{l}^{N}}{dx^2}}\right) + a \left({\sum\limits_{j = 1}^{N}{C_j \psi_j^{N}}, \psi_{l}^{N}}\right) = \eta (x).} \end{gather*}$

( 7.14)

Отсюда следует, чтобы первая сумма в (7.14) вычислялась, желательно, чтобы базисы 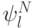${\psi}_{l}^{N}$ были гладкими:

$\begin{gather*} \psi_{l}^{N} \in W_2^2[0, X], \\ \| \psi_{l}^{N}\|_{W_2^2}^2 = \int\limits_0^{X}{\left[{(\psi_{l}^{N})^2 + \left({\frac{{d \psi_{l}^{N}}}{dx}}\right)^2 + \left({\frac{{d^2 \psi_{l}^{N}}}{{dx^2}}}\right)^2}\right]dx}, \end{gather*}$