| Россия |
Численные методы решения уравнений в частных производных гиперболического типа (на примере уравнения переноса)
и единственную на данном шаблоне схему третьего порядка аппроксимации с
порядком 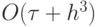 :
:
 |
( 3.16) |
Остальные коэффициенты находятся с использованием (3.15) и (3.16).
Введем пространство коэффициентов 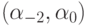 . Тогда
любая точка в этом пространстве есть разностная схема с порядком аппроксимации
. Тогда
любая точка в этом пространстве есть разностная схема с порядком аппроксимации  . Прямая (3.15) отделяет в пространстве множество схем с порядком
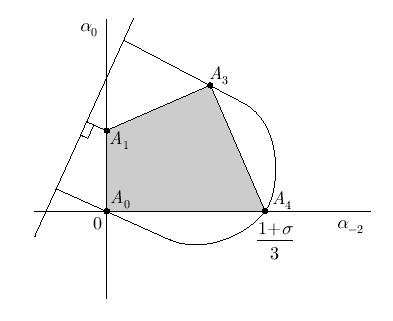
. Прямая (3.15) отделяет в пространстве множество схем с порядком 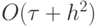 (рис.
3.2), на ней лежит единственная точка — аппроксимация
(рис.
3.2), на ней лежит единственная точка — аппроксимация 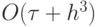 . Должна быть также и точка с порядком аппроксимации
. Должна быть также и точка с порядком аппроксимации 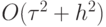 .
.
Зафиксируем какое - либо число Куранта, например,  .
Применим к разностной схеме (3.14) с неопределенными коэффициентами
спектральный признак устойчивости (фон Неймана). Получится кривая, которая определяет границу устойчивости разностных схем в пространстве неопределенных коэффициентов.
.
Применим к разностной схеме (3.14) с неопределенными коэффициентами
спектральный признак устойчивости (фон Неймана). Получится кривая, которая определяет границу устойчивости разностных схем в пространстве неопределенных коэффициентов.
Для схем первого порядка выпишем первое дифференциальное приближение:
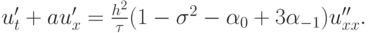
Можно также выделить множество таких схем, что  .
Это — монотонные схемы (заштрихованный многоугольник на рис. 3.2). Среди монотонных схем можно найти схему с наименьшей ошибкой аппроксимации. Это точка многоугольника, которая при данном
.
Это — монотонные схемы (заштрихованный многоугольник на рис. 3.2). Среди монотонных схем можно найти схему с наименьшей ошибкой аппроксимации. Это точка многоугольника, которая при данном  лежит ближе всего к прямой со схемами второго порядка аппроксимации.
лежит ближе всего к прямой со схемами второго порядка аппроксимации.
Закончим рассмотрение примера с модельным линейным уравнением переноса:
u't + cu'x = 0.
На выбранном шаблоне любая разностная схема, как указывалось ранее, представляется в виде

В случае монотонной схемы можно оценить норму погрешности. Заметим, что погрешность v определяется тем же разностным уравнением (3.14), тогда с использованием первой нормы (максимум абсолютной величины)
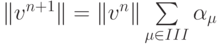
в силу аппроксимации
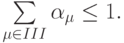
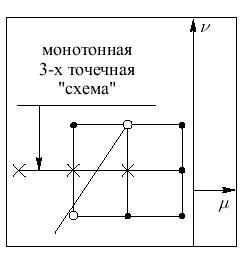
Отсюда следует, что монотонные разностные схемы всегда устойчивы. В общем случае можно рассматривать многослойные шаблоны для уравнения переноса (рис. 3.3)

и записывать условия порядка для аппроксимации соответствующего порядка:
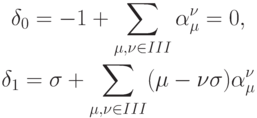
Исключая два коэффициента из условий порядка, можно от пространства неопределенных коэффициентов  перейти к пространству
перейти к пространству 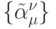 , размерность
которого на 2 меньше, например:
, размерность
которого на 2 меньше, например:

где, конечно, точки (0; - 1) и (0; 1) не включаются в суммирование. Условие устойчивости в пространстве неопределенных коэффициентов имеет вид

где q есть спектр оператора послойного перехода. Эта величина определяется из условия
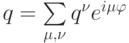
и дополнительного требования
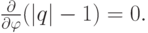
Основная гипотеза: Разностным схемам, которым в пространстве  соответствуют близкие друг к другу точки (в смысле
соответствуют близкие друг к другу точки (в смысле 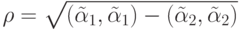 ) по своим свойствам также близки.
) по своим свойствам также близки.
Расширяя шаблон, как и в случае пятиточечного шаблона, можно строить области схем высокого порядка аппроксимации, монотонные схемы (  ) и т.д.
) и т.д.
Монотонные разностные схемы в пространстве неопределенных коэффициентов
занимают некий выпуклый многоугольник, вершины которого определяются довольно просто: это все возможные при данном числе Куранта  трехточечные разностные схемы, причем для характеристики, проходящей через
трехточечные разностные схемы, причем для характеристики, проходящей через 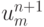 , одна точка схемы лежит выше (левее) характеристики, а другая ниже (правее), см. рис. 3.3.
, одна точка схемы лежит выше (левее) характеристики, а другая ниже (правее), см. рис. 3.3.
Метод построения разностных схем в пространстве неопределенных коэффициентов для квазилинейных систем уравнений гиперболического типа (к ним относятся системы уравнений механики сплошных сред, в частности, газовой динамики, механики деформируемого твердого тела (МДТТ) и т.п.) допускает обобщение и на многомерные случаи. Подробное описание можно найти в монографии [13.9]. Здесь же многомерные обобщения рассматриваться не будут. Они приводят к эффективным численным методам для нестационарных многомерных задач.
Исследовав схемы (3.14) на устойчивость по спектральному признаку, получаем множество устойчивых схем, а потребовав выполнения условия  для всех точек шаблона, получаем множество схем с положительной аппроксимацией (монотонных по Фридрихсу схем). На рассматриваемом
шаблоне устойчивые схемы существуют при
для всех точек шаблона, получаем множество схем с положительной аппроксимацией (монотонных по Фридрихсу схем). На рассматриваемом
шаблоне устойчивые схемы существуют при 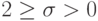 (для a > 0 ).
(для a > 0 ).
Множество схем с положительной аппроксимацией не пересекается с множеством схем с порядком аппроксимации выше первого, как это следует из теоремы С.К. Годунова.
Первое дифференциальное приближение. Дисперсионная и диссипативная ошибки
Поскольку решения дифференциальной задачи и разностного уравнения принадлежат разным функциональным пространствам, что порождает определенные трудности при теоретическом анализе свойств разностных схем, для такого исследования возможно рассматривать разностные операторы в том же пространстве. Будем считать, что разностные схемы удовлетворяются функциями непрерывного аргумента в каждой точке рассматриваемой области.
Обычно ограничиваются рассмотрением уравнений, в которых оставлены члены в
разложении в ряд Тейлора проекции точного решения на сетку по  и h, порядок которых совпадает с порядком погрешности аппроксимации схемы. Получающиеся при этом уравнения называют первым дифференциальным
приближением (ПДП).
и h, порядок которых совпадает с порядком погрешности аппроксимации схемы. Получающиеся при этом уравнения называют первым дифференциальным
приближением (ПДП).
Для схемы первого порядка (5) при выполнении условия (6) первым дифференциальным приближением будет
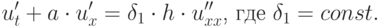 |
( 3.17) |
Из уравнения (3.17) исключены члены со второй производной u'tt, с использованием так называемой продолженной системы:
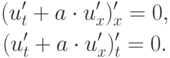
Иногда уравнение (3.17) называют  - формой (параболической формой) первого дифференциального приближения. Если производные по времени не исключаются из ПДП, то имеем Г - форму (гиперболическую
форму) ПДП, которая, как правило, не применяется в исследованиях как малоинформативная.
- формой (параболической формой) первого дифференциального приближения. Если производные по времени не исключаются из ПДП, то имеем Г - форму (гиперболическую
форму) ПДП, которая, как правило, не применяется в исследованиях как малоинформативная.
При  уравнение (3.17) можно трактовать как
присутствие в схеме некоторой диссипации ( схемной вязкости ). Ее наличие проявляется в расчетах в виде размазывания точного решения, причем его интенсивность увеличивается при ухудшении аппроксимации (увеличении шага h ). В этом случае говорят, что ошибка схемы носит диссипативный характер. Если схемная вязкость получается отрицательной, то приходим к обратной задаче теплопроводности. Как известно из курсов математической физики, такая задача поставлена некорректно. А соответствующая разностная схема при исследовании по спектральному признаку оказывается неустойчивой — по ПДП можно сделать вывод об устойчивости схемы.
уравнение (3.17) можно трактовать как
присутствие в схеме некоторой диссипации ( схемной вязкости ). Ее наличие проявляется в расчетах в виде размазывания точного решения, причем его интенсивность увеличивается при ухудшении аппроксимации (увеличении шага h ). В этом случае говорят, что ошибка схемы носит диссипативный характер. Если схемная вязкость получается отрицательной, то приходим к обратной задаче теплопроводности. Как известно из курсов математической физики, такая задача поставлена некорректно. А соответствующая разностная схема при исследовании по спектральному признаку оказывается неустойчивой — по ПДП можно сделать вывод об устойчивости схемы.
Для более высокого (второго) порядка ПДП имеет вид
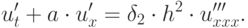 |
( 3.18) |
Уравнение (3.18) обладает дисперсией, т.е. разные пространственные гармоники разложения начального возмущения в ряд Фурье распространяются по сетке с разными скоростями. Говорят, что ошибка носит дисперсионный характер. Сеточная дисперсия легко получается, если искать частное решение последнего уравнения в виде комплексной экспоненты:  . Подробнее о ПДП в [13.4].
. Подробнее о ПДП в [13.4].
Интересна связь ПДП и исследования свойств схем в пространствах неопределенных коэффициентов. Так, для схем первого порядка расстояние от точки в пространстве неопределенных коэффициентов до прямой схем высокого порядка (3.15) по абсолютной
величине равен коэффициенту 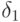 в уравнении (3.17), а знак определяется положением внутри области устойчивости.
в уравнении (3.17), а знак определяется положением внутри области устойчивости.
Численные расчеты по разностным схемам высокого порядка показывают, что осцилляции нефизического характера появляются в окрестности разрывов решения или его первой производной. В связи с этим возникает идея построения численного метода, имеющего высокий порядок аппроксимации на участках гладкого решения, в то время как в окрестности разрывов функций или их производных применяется монотонная схема (с положительной аппроксимацией) первого порядка.
Можно формализовать этот подход:
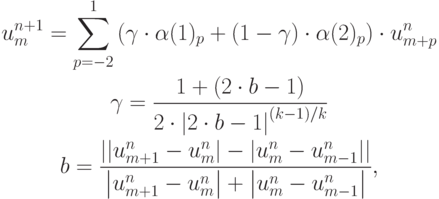
где 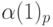 — коэффициенты первой схемы (высокого
порядка аппроксимации), применяемой в области гладкого решения,
— коэффициенты первой схемы (высокого
порядка аппроксимации), применяемой в области гладкого решения,  — коэффициенты второй (монотонной) схемы,
— коэффициенты второй (монотонной) схемы,  — весовой коэффициент, вспомогательный параметр b характеризует гладкость решения (очевидно, что b = 0, при
— весовой коэффициент, вспомогательный параметр b характеризует гладкость решения (очевидно, что b = 0, при  ), k — коэффициент гибридности — целое число из диапазона
), k — коэффициент гибридности — целое число из диапазона  .
.
При этом реализовано достаточно гладкое переключение со схем высокого порядка аппроксимации на монотонные схемы.