| Россия |
Численные методы решения уравнений в частных производных гиперболического типа (на примере уравнения переноса)
3.9. Задачи
- Для линейного уравнения переноса

предложить схему N + 1 порядка аппроксимации.
Указание. Рассмотреть невязку, образующуюся при замене дифференциального уравнения разностным
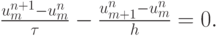
Решение. Проведем исследование разностного уравнения на аппроксимацию. Для этого представим сеточные функции
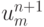 и
и  в виде разложения проекции на сетку точного решения дифференциальной задачи в ряд Тейлора:
в виде разложения проекции на сетку точного решения дифференциальной задачи в ряд Тейлора: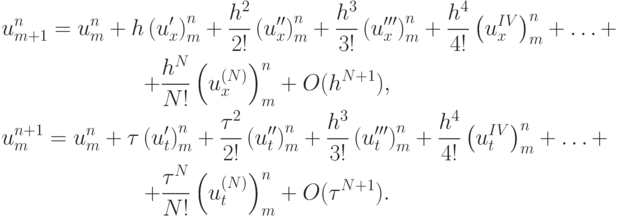
Отсюда получим с учетом того, что
 :
: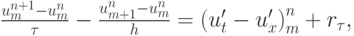
где
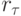 — невязка, вычисляемая в точке (tn, xm) по формуле
— невязка, вычисляемая в точке (tn, xm) по формуле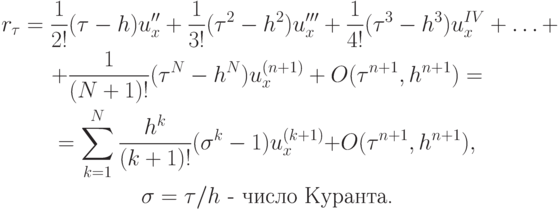
Аппроксимация частных производных высоких порядков, входящих в выражение для невязки с помощью конечных разностей, приводит к соотношению
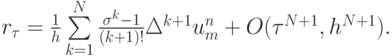
В таком случае, после переноса суммы по k в выражении для невязки в левую часть, получим разностную схему искомого порядка аппроксимации:
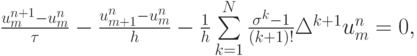
или
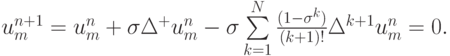
Эта схема легко распространяется на уравнение

если учесть, что
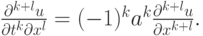
- Доказать устойчивость разностной схемы
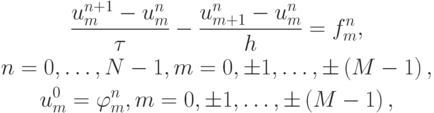
аппроксимирующую задачу Коши для уравнения переноса
![\begin{gather*}
\frac{{\partial}u}{{\partial}t} - \frac{{\partial}u}{{\partial}x} = f(t, x) t \in \left[{0, T}\right],\\
x \in (- \infty , \infty ), \quad u(0, x) = {\varphi}(x), \quad x \in \left({- \infty , \infty }\right),
\end{gather*}](/sites/default/files/tex_cache/a61b074af42c47d3d298976096ac9759.png)
используя второе определение устойчивости:

Решение. Перепишем разностную схему в виде, разрешенном относительно следующего слоя по времени
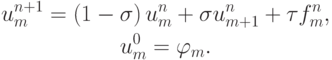
Определим норму в пространстве сеточных функций как

Если
 , то справедлива оценка
, то справедлива оценка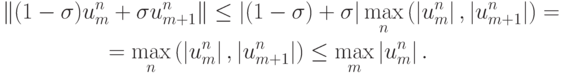
В таком случае
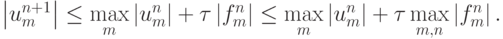
Отсюда видно, что при
 норма решения
норма решения 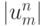 не возрастает при возрастании n — выполняется
принцип максимума. Поскольку правая часть в полученном неравенстве не зависит от m, то
не возрастает при возрастании n — выполняется
принцип максимума. Поскольку правая часть в полученном неравенстве не зависит от m, то  .
.Аналогично

Сложение этих неравенств дает
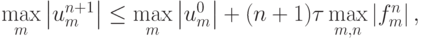
откуда получаем, с учетом того, что
 :
:
При этом учтено, что
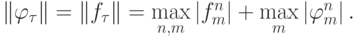
Таким образом, получим
 .
. - Построить явную разностную схему первого порядка точности для аппроксимации линейного уравнения переноса используя ее запись в общем виде через неопределенные коэффициенты

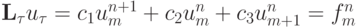 ,
,на шаблоне "явный правый уголок".
Решение. Будем подбирать коэффициенты ci таким образом, чтобы выполнялось условие аппроксимации первого порядка
 .
.Разложение сеточных функций
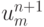 и
и 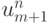 в ряды Тейлора в окрестности точки xm, tn приводит к равенствам
в ряды Тейлора в окрестности точки xm, tn приводит к равенствам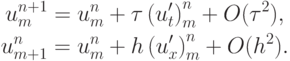
Подстановка этих разложений в разностную схему с неопределенными коэффициентами дает
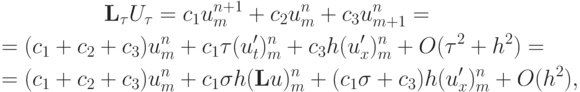
поскольку можно считать независимыми переменными шаг по пространству и число Куранта, а для шага по времени получаем очевидное выражение
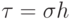 ,
, 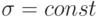 .
.Здесь использованы очевидные равенства для дифференциального оператора
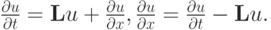
Для выполнения условия аппроксимации первого порядка

необходимо выполнение условий порядка

Если положить O(h) = 0, поскольку это некое число, стремящееся к нулю при измельчении шага, то условия порядка примут вид
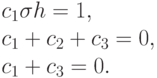
Эта схема линейных алгебраических уравнений имеет единственное решение:

Получили коэффициенты уже известной разностной схемы первого порядка аппроксимации на заданном шаблоне:
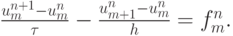
Несложно проверить, что учет O(h) привел бы к незначительной коррекции результата.
Конечно, выбранная разностная схема легко получается и из других соображений. Но с помощью метода неопределенных коэффициентов удается построить схемы с хорошими свойствами для более сложных уравнений и систем.