| Россия |
Численные методы решения уравнений в частных производных гиперболического типа (на примере уравнения переноса)
- Исследовать на спектральную устойчивость разностную схему на шаблоне квадрат
![\begin{gather*} \frac{1}{{2{\tau}}} \left[{(u_{m + 1}^{n + 1} + u_m^{n + 1}) - (u_{m + 1}^{n} - u_m^{n})}\right] + \\
+ \frac{1}{h} \left[{(u_{m + 1}^{n + 1} + u_{m + 1}^{n}) - (u_m^{n + 1} - u_m^{n})}\right] = f_{m + 1/2}^{n + 1/2}, \end{gather*}](/sites/default/files/tex_cache/ff0b94787ab941a57921fd8b551b6b4c.png)
аппроксимирующую линейное уравнение переноса

Решение. После подстановки в схему гармоник Фурье

получим выражение для спектра оператора послойного перехода

Тогда
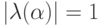 и рассматриваемая схема безусловно устойчива. Этого следовало ожидать, так как аппроксимация производной по времени производится как на нижнем, так и на верхнем временном слое. Однако решение на верхнем слое выписывается в явном виде, поскольку правое условие ставится на левой границе. Поэтому схему иногда относят к явным схемам бегущего счета. Расчетная формула будет
и рассматриваемая схема безусловно устойчива. Этого следовало ожидать, так как аппроксимация производной по времени производится как на нижнем, так и на верхнем временном слое. Однако решение на верхнем слое выписывается в явном виде, поскольку правое условие ставится на левой границе. Поэтому схему иногда относят к явным схемам бегущего счета. Расчетная формула будет
Схема обладает вторым порядком аппроксимации по времени и пространственной координате.
- Получить дисперсионное соотношение для разностных схем первого и второго порядка сходимости для аппроксимации нелинейного уравнения

и, вообще говоря, зависит от решения.
Указание. Использовать дисперсионное соотношение для данного дифференциального уравнения в виде
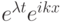 , где k — волновое число,
, где k — волновое число,  .
.Решение. Будем искать дисперсионное соотношение для разностного уравнения в виде

После его подстановки в схему правый уголок первого порядка аппроксимации, получим

откуда следует

Сравним дисперсионное соотношение для дифференциального и соответствующих разностных уравнений.
Пусть
Имеет место совпадение
 и
и  , однако этот случай мало интересен для вычислительной практики, поскольку u может меняться в ходе решения задачи. Для проведения дисперсионного анализа схем положим
, однако этот случай мало интересен для вычислительной практики, поскольку u может меняться в ходе решения задачи. Для проведения дисперсионного анализа схем положим  , имея в виду то, что h — малый параметр, а аппроксимация тем лучше, чем меньше волновое число, т.е. чем более гладким является исследуемое частное решение. Заметим, что для расчетной сетки с шагом h обычно реализуются волновые числа
, имея в виду то, что h — малый параметр, а аппроксимация тем лучше, чем меньше волновое число, т.е. чем более гладким является исследуемое частное решение. Заметим, что для расчетной сетки с шагом h обычно реализуются волновые числа  .
.
В таком случае дисперсионное соотношение будет


Первый сомножитель совпадает с соответствующим частным решением дифференциального уравнения, второй является особенностью разностного решения; его поведение при различных
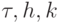 представляет особенный
интерес. При u < 0,
представляет особенный
интерес. При u < 0,  , как видно из этого решения, рассматриваемую схему нельзя использовать для проведения расчетов. Второй сомножитель имеет порядок exp (k2 | u | htn), он быстро растет при
, как видно из этого решения, рассматриваемую схему нельзя использовать для проведения расчетов. Второй сомножитель имеет порядок exp (k2 | u | htn), он быстро растет при  . Аналогичная ситуация получается и при u > 0,
. Аналогичная ситуация получается и при u > 0,  . При u < 0,
. При u < 0,  второй сомножитель затухает с ростом tn тем быстрее, чем больше k, или чем меньше
второй сомножитель затухает с ростом tn тем быстрее, чем больше k, или чем меньше  — длина волны частного решения вида exp(ikx). Таким образом, численное решение, полученное по схеме уголок, отличается от точного, в котором все гармоники сохраняют амплитуду с ростом tn, наличием затухающего множителя для гармоник с большими волновыми числами (или малыми длинами волн).
Действие этого сомножителя приводит к сглаживанию решений, имеющих разрыв в начальных данных.
— длина волны частного решения вида exp(ikx). Таким образом, численное решение, полученное по схеме уголок, отличается от точного, в котором все гармоники сохраняют амплитуду с ростом tn, наличием затухающего множителя для гармоник с большими волновыми числами (или малыми длинами волн).
Действие этого сомножителя приводит к сглаживанию решений, имеющих разрыв в начальных данных.Для разностной схемы Лакса - Вендроффа второго порядка

дисперсионное соотношение будет

для длинноволновых гармоник с

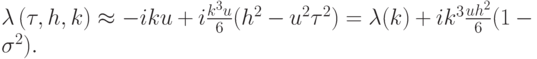
Из полученных соотношений можно сделать следующий вывод. Решения исходного уравнения переноса имеют вид волн с волновым числом k, которые движутся вправо со скоростью u, так как

Решения разностного уравнения имеют вид
![\begin{gather*} v \left({t_n , x_m }\right) = \exp ({ikx}_m +
{\lambda}({\tau}, {h, k})t_n ) = \\
= \exp \left({ik \left\{{x_m - u \left[{1 - \frac{{k^2}}{6} \left({h^2 - u^2{\tau}^2}\right)}
\right]t_n }\right\}}\right) = \\
= \exp \left({ik \left\{{x_m - u \left[{1 + {U}_k (k)}\right]t_n }\right\}}\right),
\end{gather*}](/sites/default/files/tex_cache/ab25abb93c2324b33174d35c8d107899.png)
где введено обозначение

Последнее выражение означает, что разностные решения уже не имеют вид волн, движущихся с одной и той же скоростью. Теперь каждая волна со своей частотой движется с собственной скоростью u = Uk[1 + u(k)]. Разумеется, при малых k и скорости uk мало отличаются от u, но высокочастотные волны движутся со скоростями, заметно отличающимися от скорости переноса. Кроме того, в схеме Лакса - Вендроффа гармоники со временем не затухают, численное решение не сглаживается со временем. Начальный волновой пакет u и определенный им начальный профиль решения, изменяются с течением времени из - за рассогласования фаз. Это приводит к потере монотонности профиля v(x), если он был вначале монотонным, и появлению осцилляций разностного происхождения. Появление сеточной дисперсии — одно из проявлений эффекта Гиббса, подробнее об эффекте Гиббса в [13.16].
- Акустическая система описывает распространение плоских звуковых волн. Поставим для нее задачу Коши:

где u — скорость движения среды, p — давление,
 - плотность среды, c — скорость звука в среде.
- плотность среды, c — скорость звука в среде.- a) Представить акустическую систему в интегральной форме.
- b) Преобразовать акустическую систему к виду системы с разделенными переменными.
- c) Предложить разностную схему первого порядка точности для ее решения.
Решение.
- a) Проинтегрировав акустическую систему по произвольной области с границей G, получим:

- b) Умножим второе уравнение на
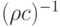 , затем сложим с первым и вычтем из него. Получим систему двух уравнений
, затем сложим с первым и вычтем из него. Получим систему двух уравнений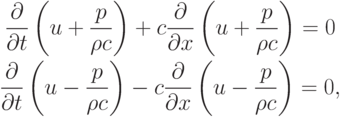
или, после введения обозначений (инвариантов Римана)
система запишется в виде двух уравнений переноса: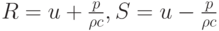

Эта система позволяет выписать общее решение:
R = f(x - ct), S = g(x + ct).
Здесь f, g — произвольные непрерывно дифференцируемые функции, определяемые из начальных условий. В терминах инвариантов Римана можно определить и значения естественных переменных u, p:

Замечательное свойство инвариантов Римана R, S заключается в их постоянстве вдоль прямых x - ct = const, и x + ct = const или
— характеристик акустической системы.
Если задавать начальные данные
 ,
,  , то связь начальных данных
и инвариантов Римана будет
, то связь начальных данных
и инвариантов Римана будет![$ {\varphi}\left(x\right) = \frac{1}{2}(f(x) + g(x)), {\psi}(x) = \frac{{\rho}c}{2} \left[{f(x) - g(x)}\right], $](/sites/default/files/tex_cache/59f97f41db9b358ecb91c619b4347a2b.png)
откуда получим

Следовательно, решение системы в этом случае

Для численного решения системы, записанной в инвариантах Римана, можно применить схему Куранта - Изаксона - Риса:

или
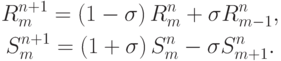
Известно, что данная схема имеет первый порядок аппроксимации и является устойчивой при выполнении условия КФЛ:

- Заменить смешанную задачу для волнового уравнения

эквивалентной ему парой уравнений в частных производных первого порядка.
Решение. Введем новые переменные

Функции u(t, x), v(t, x), что несложно проверить, удовлетворяют акустической системе уравнений

Введем в рассмотрение параметрическую схему для численного решения этой системы:

Исследование полученной двухпараметрической разностной схемы на спектральную устойчивость дает условия устойчивости:
Отсюда видно, что если
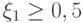 и
и  , то схема устойчива при любых числах Куранта и сеточных параметрах,
если
, то схема устойчива при любых числах Куранта и сеточных параметрах,
если  , но один из параметров меньше 0, 5, то схема условно устойчива при
, но один из параметров меньше 0, 5, то схема условно устойчива при 
Пусть
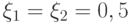 . Тогда полученная схема является безусловно устойчивой и обладает вторым порядком аппроксимации по обоим переменным.
. Тогда полученная схема является безусловно устойчивой и обладает вторым порядком аппроксимации по обоим переменным. - Исследовать на сходимость схему "крест" с шаблоном
для численного решения волнового уравнения

Решение. Запишем разностную схему:

Исследование на аппроксимацию дает выражение для главного члена невязки

Схема имеет второй порядок аппроксимации. Исследуем схему на устойчивость по спектральному признаку. Для спектра оператора послойного перехода получается
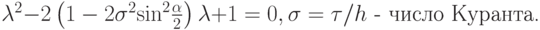
По теореме Виета, произведение корней
 , и условие устойчивости выполняется, если
, и условие устойчивости выполняется, если  .
Для полученного квадратного уравнения с действительными коэффициентами это означает, что его корни являются комплексно сопряженными. Это возможно лишь в случае, если дискриминант
.
Для полученного квадратного уравнения с действительными коэффициентами это означает, что его корни являются комплексно сопряженными. Это возможно лишь в случае, если дискриминант
будет отрицательным. Условие устойчивости будет выполнено для всех гармоник, если
 .
.

