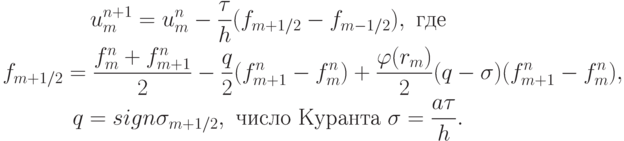НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 3: Численные методы решения уравнений в частных производных гиперболического типа (на примере уравнения переноса)

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: профессионал | Доступ: платный

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать программу

3.6. Гибридные схемы (метод Р.П.Федоренко)

Идею построения гибридных схем, изложенную в [13.11], рассмотрим на традиционном примере схемы "уголок"

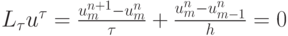
$L_{\tau} u^{\tau} = \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + \frac{{u_m^{n} - u_{m - 1}^{n}}}{h} = 0$

для численного решения модельного уравнения переноса

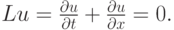
$Lu = \frac{{\partial}u}{{\partial}t} + \frac{{\partial}u}{{\partial}x} = 0.$

Разложения сеточных функций проекции на сетку точного решения дифференциальной задачи в ряд Тейлора дает

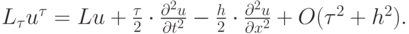
$L_{\tau} u^{\tau} = Lu + \frac{\tau}{2} \cdot \frac{{{\partial}^2 u}}{{{\partial}t^2}} - \frac{h}{2} \cdot \frac{{{\partial}^2 u}}{{{\partial}x^2}} + O({\tau}^2 + h^2 ).$

Поскольку

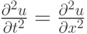
$\frac{{{\partial}^2 u}}{{{\partial}t^2}} = \frac{{{\partial}^2 u}}{{{\partial}x^2}}$

, что показывается дифференцированием рассматриваемого уравнения переноса по t и по x, полученное выражение может быть представлено в виде

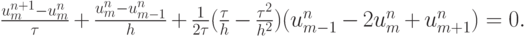
$\frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + \frac{{u_m^{n} - u_{m - 1}^{n}}}{h} + \frac{1}{{2{\tau}}}(\frac{\tau}{h} - \frac{{{\tau}^2}}{{h^2}})(u_{m - 1}^{n} - 2u_m^{n} + u_{m + 1}^{n}) = 0.$

Аналогичным образом можно получить и схему третьего порядка точности:

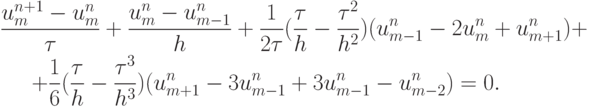
$\begin{gather*} \frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + \frac{{u_m^{n} - u_{m - 1}^{n}}}{h} + \frac{1}{{2{\tau}}}(\frac{\tau}{h} - \frac{{{\tau}^2}}{{h^2}})(u_{m - 1}^{n} - 2u_m^{n} + u_{m + 1}^{n}) + \\ + \frac{1}{6}(\frac{\tau}{h} - \frac{{{\tau}^3 }}{{h^3 }})(u_{m + 1}^{n} - 3u_{m - 1}^{n} + 3u_{m - 1}^{n} - u_{m - 2}^{n}) = 0. \end{gather*}$

Введем разностный анализатор гладкости численного решения, сравнивая конечные разности первого и второго порядков:

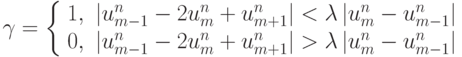
$\gamma = \left\{ \begin{array}{cc} 1, & \left|{u_{m - 1}^{n} - 2u_m^{n} + u_{m + 1}^{n}}\right| < {\lambda}\left|{u_m^{n} - u_{m - 1}^{n}}\right| \\ 0, & \left|{u_{m - 1}^{n} - 2u_m^{n} + u_{m + 1}^{n}}\right| > {\lambda}\left|{u_m^{n} - u_{m - 1}^{n}}\right| \\ \end{array} \right.$

и представим полученную схему в виде:

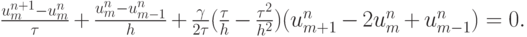
$\frac{{u_m^{n + 1} - u_m^{n}}}{\tau} + \frac{{u_m^{n} - u_{m - 1}^{n}}}{h} + \frac{\gamma }{{2{\tau}}}(\frac{\tau}{h} - \frac{{{\tau}^2}}{{h^2}})(u_{m + 1}^{n} - 2u_m^{n} + u_{m - 1}^{n}) = 0.$

Таким образом, в областях с большим градиентом численного решения 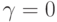$\gamma = 0$ и расчет ведется по схеме первого порядка точности, в области же гладкого решения 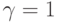$\gamma = 1$ и расчет ведется по схеме второго порядка, (при 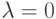$\lambda = 0$ имеем схему первого, при 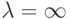${\lambda} = \infty$ - второго порядка точности). Аналогичный анализатор можно ввести и для схемы третьего порядка аппроксимации.

Заметим, что гибридные схемы, построенные выше для аппроксимации линейного уравнения переноса , уже нелинейные — коэффициенты переключения зависят от локальных свойств решения. Таким образом, в соответствие линейному дифференциальному оператору ставится нелинейный. Для таких схем не обязана выполняться теорема С.К.Годунова, и можно ожидать, что на пути введения нелинейности для гиперболических систем и уравнений можно построить монотонные или близкие к монотонным схемы высокого порядка аппроксимации.

3.7. Схемы с уменьшением полной вариации (Total Variation Diminishing, схемы Хартена)

Схемы с уменьшением полной вариации (сокращенно их называют TVD - схемами ) описаны, например, в [13.8], [13.12]. Для построения схемы рассмотрим полную вариацию численного решения. Она определяется следующим образом:

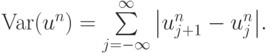$$ {{\rm Var}(u^{n}) = \sum\limits_{j = - \infty }^ \infty {\left|{u_{j + 1}^{n} - u_j^{n}}\right|}.}$

( 3.9)

Схема будет TVD, если

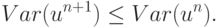${Var}(u^{n + 1}) \le {Var}(u^{n}).}$

( 3.10)

Суть построения TVD - схем можно понять, представив схему Лакса - Вендроффа для численного решения модельного уравнения переноса в виде

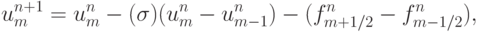${u_m^{n + 1} = u_m^{n} - ({\sigma})(u_m^{n} - u_{m - 1}^{n}) - (f_{m + 1/2}^{n} - f_{m - 1/2}^{n}), }$

( 3.11)

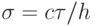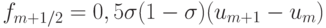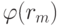где $\sigma = c\tau /h$ , $f_{m + 1/2} = 0, 5\sigma (1 - \sigma )(u_{m + 1} - u_{m})$ — антидиффузионные потоки. Схема похожа на метод коррекции потоков, но одношаговый. Эта схема не монотонна. Сделаем ее монотонной, ограничив антидиффузионные потоки введением функций ${\varphi}(r_m )$ :

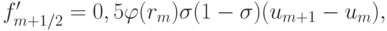
$f^{\prime}_{m + 1/2} = 0, 5 \varphi(r_m) \sigma(1 - \sigma)(u_{m + 1} - u_m),$

аналогично для f'_{m - 1/2}. Здесь $\varphi$ — ограничитель,

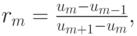
$r_m = \frac{{u_m - u_{m - 1}}}{{u_{m + 1} - u_m }},$

отношение прилежащих градиентов 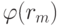${\varphi}(r_m )$ выбирается так, чтобы (3.11) была TVD - схемой, причем в расчетах обычно полагают

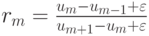
$r_m = \frac{u_m - u_{m - 1} + \varepsilon }{u_{m + 1} - u_m + \varepsilon }$

, где $\varepsilon$ — малое число.

Можно показать, что условием устойчивости схемы является неравенство

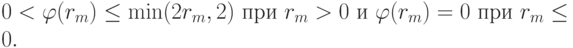
$0 < {\varphi}(r_m ) \le \min (2r_m , 2) \mbox{ при } r_m > 0 \mbox{ и } {\varphi}(r_m ) = 0 \mbox{ при } r_m \le 0.$

Простейшим ограничителем является выбор конечных разностей в соответствии с принципом минимальных производных Колгана:

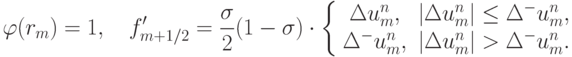
$\begin{gather*} {\varphi}(r_m ) = 1, \quad f^{\prime}_{m + 1/2} = \frac{{\sigma}}{2}(1 - {\sigma}) \cdot \left\{ \begin{array}{cc} {{\Delta}u_m^{n}, & \left| {{\Delta}u_m^{n}}\right| \le {\Delta}^{-} u_m^{n}, } \\ {{\Delta}^{-} u_m^{n}, & \left|{{\Delta}u_m^n}\right| > {\Delta}^{-} u_m^{n} .} \\ \end{array} \right. \end{gather*}$

Приведем пример другого ограничителя:

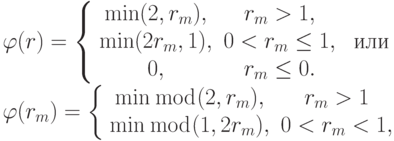
$\varphi(r) = \left\{ \begin{array}{cc} {\min (2, r_m), & r_m > 1, } \\ {\min (2r_m, 1), & 0 < r_m \le 1, } \\ {0, & r_m \le 0.} \end{array} \right. \mbox{ или } \\ {\varphi}(r_m ) = \left\{ \begin{array}{cc} {\min\bmod (2, r_m ), & r_m > 1} \\ {\min\bmod (1, 2r_m ), & 0 < r_m < 1, } \\ \end{array} \right.$

где

$\min\bmod ({x, y}) = \frac{sign{x} + sign{y}}{2} \min (\left|{x}\right|, \left|{y}\right|).$

Пояснение.

r_m > 1: u_m - u_{m - 1} > u_{m + 1} - u_m (если и числитель, и знаменатель в выражении для r_m положительны) или u_{m - 1} - u_m > u_m - u_{m + 1} (если и числитель, и знаменатель отрицательны); численное решение сглаживается, так как его градиент убывает.

или
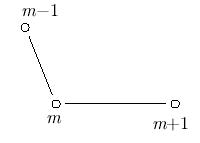
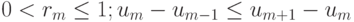$0 < r_m \le 1; u_m - u_{m - 1} \le u_{{m} + 1} - u_m$ (если и числитель, и знаменатель в выражении для r_m положительны) или u_{m - 1} - u_m < u_m - u_{m + 1} (если и числитель, и знаменатель отрицательны); градиент численного решения растет (или не убывает).
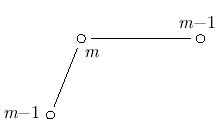
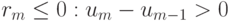$r_m \le 0: u_m - u_{m - 1} > 0$ и u_{m + 1} - u_m < 0, или u_m - u_{m - 1} < 0 и u_{m + 1} - u_m > 0, — численное решение осциллирует.

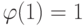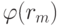Для обеспечения второго порядка точности необходимо ${\varphi}(1) = 1$ . Различные TVD - алгоритмы соответствуют различному выбору ${\varphi}(r_m )$ .

Дивергентный вариант TVD - схемы:

$\begin{gather*} u_m^{n + 1} = u_m^n - \frac{\tau}{h}(f_{m + 1/2} - f_{m - 1/2}), \mbox{ где} \\ f_{m + 1/2} = \frac{f_m^n + f_{m + 1}^n}{2} - \frac{q}{2}(f_{m + 1}^n - f_m^n) + \frac{{\varphi}(r_m )}{2}(q - {\sigma})(f_{m + 1}^n - f_m^n), \\ q = sign \sigma_{m + 1/2}, \mbox{ число Куранта } \sigma = \frac{a{\tau}}{h}. \end{gather*}$