Основные понятия теории графов
Определение графа
Графом  называется пара
называется пара  ,
где
,
где  — непустое конечное множество элементов, называемых вершинами, а
— непустое конечное множество элементов, называемых вершинами, а 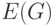 —
конечное семейство неупорядоченных пар элементов из
—
конечное семейство неупорядоченных пар элементов из  (необязательно различных),
называемых ребрами. Употребление слова "семейство" говорит о том,
что допускаются кратные ребра. Будем называть
(необязательно различных),
называемых ребрами. Употребление слова "семейство" говорит о том,
что допускаются кратные ребра. Будем называть  " множеством вершин "
, а
" множеством вершин "
, а 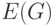 — семейством
ребер графа
— семейством
ребер графа  . О каждом ребре вида
. О каждом ребре вида  говорят, что оно соединяет вершины
говорят, что оно соединяет вершины  и
и 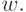 Каждая
петля
Каждая
петля  соединяет вершину
соединяет вершину  саму с собой.
саму с собой.
При изображении графов на рисунках или схемах отрезки могут быть прямолинейными или криволинейными; длины отрезков и расположение точек произвольны.
Определение орграфа
Орграфом 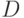 называется пара
называется пара  , где
, где  — непустое конечное множество элементов, называемых вершинами, а
— непустое конечное множество элементов, называемых вершинами, а 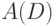 — конечное семейство упорядоченных пар
элементов из
— конечное семейство упорядоченных пар
элементов из  , называемых дугами (или ориентированными ребрами ). Дуга, у которой
вершина
, называемых дугами (или ориентированными ребрами ). Дуга, у которой
вершина  является первым элементом, а вершина
является первым элементом, а вершина  — вторым,
называется дугой из
— вторым,
называется дугой из  в
в 
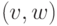 .
Заметим, что дуги
.
Заметим, что дуги 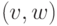 и
и  различны. Хотя
графы и орграфы —
существенно различные объекты, в определенных случаях графы можно
рассматривать как орграфы, в которых каждому ребру соответствуют две
противоположно ориентированные дуги.
различны. Хотя
графы и орграфы —
существенно различные объекты, в определенных случаях графы можно
рассматривать как орграфы, в которых каждому ребру соответствуют две
противоположно ориентированные дуги.
Полный граф
Граф называется полным, если
каждые две различные вершины его соединены одним и только одним ребром.
В полном графе каждая его вершина принадлежит одному и тому же числу
ребер. Для задания полного графа достаточно знать число его вершин. Полный
граф с  вершинами обычно обозначается через
вершинами обычно обозначается через 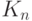 .
.
Граф, не являющийся полным, можно преобразовать в полный с теми же
вершинами, добавив недостающие ребра. Вершины графа  и ребра,
которые добавлены, тоже образуют граф. Такой граф называют дополнением
графа
и ребра,
которые добавлены, тоже образуют граф. Такой граф называют дополнением
графа  и обозначают его
и обозначают его 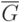 .
.
Дополнением графа  называется граф
называется граф 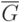 с теми же
вершинами, что и граф
с теми же
вершинами, что и граф  , и с теми и только теми ребрами, которые
необходимо добавить к графу
, и с теми и только теми ребрами, которые
необходимо добавить к графу  , чтобы получился полный граф.
, чтобы получился полный граф.
Является граф полным или нет, это его характеристика в целом.
Полный ориентированный граф
Полным ориентированным графом называется граф, каждая пара вершин которого соединена в точности одним ориентированным ребром. Если с каждого ребра полного ориентированного графа снять направление, то образуется полный граф с неориентированными ребрами.
Рассмотрим соревнование, в котором каждая из команд играет с каждой из остальных команд по одному разу. Такое соревнование называют круговым турниром или турниром в один круг.
Если каждая встреча непременно должна оканчиваться выигрышем одной из команд, то круговой турнир называют бескомпромиссным. Круговой бескомпромиссный турнир проводится, например, в волейболе и баскетболе.

Каждому турниру соответствует полный ориентированный граф, в котором
вершины представляют команды, а каждое ориентированное ребро  выражает
отношение "
выражает
отношение "  победила
победила  ".
".
