Основные понятия теории графов
Двудольный граф
Допустим, что множество вершин графа можно разбить на два
непересекающихся подмножества 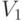 и
и 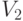 , так,
что каждое ребро в
, так,
что каждое ребро в  соединяет какую-нибудь вершину из
соединяет какую-нибудь вершину из 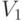 с какой-либо вершиной из
с какой-либо вершиной из 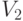 , тогда
, тогда  называем двудольным графом.
Такие графы иногда обозначают
называем двудольным графом.
Такие графы иногда обозначают 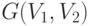 , если хотят выделить
два указанных подмножества. Двудольный граф можно определить и по-другому: в
терминах раскраски его вершин двумя цветами, скажем, красным и синим. При
этом граф называется двудольным, если каждую его вершину можно окрасить
красным или синим цветом так, чтобы любое ребро имело один конец красный,
а другой — синий. Следует подчеркнуть, что в двудольном графе совсем не
обязательно каждая вершина из
, если хотят выделить
два указанных подмножества. Двудольный граф можно определить и по-другому: в
терминах раскраски его вершин двумя цветами, скажем, красным и синим. При
этом граф называется двудольным, если каждую его вершину можно окрасить
красным или синим цветом так, чтобы любое ребро имело один конец красный,
а другой — синий. Следует подчеркнуть, что в двудольном графе совсем не
обязательно каждая вершина из 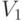 соединена с каждой вершиной
из
соединена с каждой вершиной
из 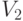 ; если же это так и если при этом граф
; если же это так и если при этом граф  простой, то он называется полным двудольным графом и обычно
обозначается
простой, то он называется полным двудольным графом и обычно
обозначается 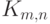 , где
, где 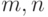 — число вершин
соответственно в
— число вершин
соответственно в 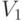 и
и 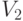 .
.
Пример.
Заметим, что граф 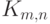 имеет ровно
имеет ровно  вершин и
вершин и  ребер.
ребер.
Степень вершины
Вершины в графе могут отличаться друг от друга тем, скольким ребрам они принадлежат.
Степенью вершины называется
число ребер графа, которым принадлежит эта вершина. Вершина называется четной, если ее степень — число четное. Вершина называется нечетной,
если ее степень — число нечетное. Две вершины
графа называются смежными, если существует
соединяющее их ребро, то есть ребро вида  ; при этом вершины
; при этом вершины  и
и  называются инцидентными этому ребру, а ребро — инцидентным этим вершинам. Аналогично, два различных ребра графа
называются смежными, если они имеют, по крайней мере, одну
общую вершину. Иначе можно определить степень вершины. Степенью или валентностью вершины
называются инцидентными этому ребру, а ребро — инцидентным этим вершинам. Аналогично, два различных ребра графа
называются смежными, если они имеют, по крайней мере, одну
общую вершину. Иначе можно определить степень вершины. Степенью или валентностью вершины  графа
графа  называется число ребер,
инцидентных
называется число ребер,
инцидентных  ; степень вершины будем обозначать через
; степень вершины будем обозначать через  . При
вычислении степени вершины
. При
вычислении степени вершины  будем учитывать петлю
в
будем учитывать петлю
в  два раза, а
не один. Вершина степени
два раза, а
не один. Вершина степени  называется изолированной вершиной, вершина степени
называется изолированной вершиной, вершина степени  называется висячей, или концевой, вершиной. Граф, у которого все
вершины имеют одну и ту же степень, называется регулярным графом.
называется висячей, или концевой, вершиной. Граф, у которого все
вершины имеют одну и ту же степень, называется регулярным графом.
Два графа,  и
и 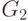 , называются изоморфными, если существует взаимно однозначное соответствие между
множествами их вершин, обладающее тем свойством, что число ребер,
соединяющих любые две вершины в
, называются изоморфными, если существует взаимно однозначное соответствие между
множествами их вершин, обладающее тем свойством, что число ребер,
соединяющих любые две вершины в  равно числу ребер,
соединяющих соответствующие вершины в
равно числу ребер,
соединяющих соответствующие вершины в 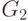 .
.
Имея даже общие представления о графе, иногда можно судить о степенях его вершин. Так, степень каждой вершины полного графа на единицу меньше числа его вершин. При этом некоторые закономерности, связанные со степенями вершин, присущи не только полным графам.
1. В графе  сумма степеней всех его вершин — число четное, равное
удвоенному числу ребер графа, так как каждое ребро участвует в этой сумме
ровно два раза. Этот результат, известный еще более двухсот лет назад Эйлеру,
часто называют леммой о рукопожатиях. Из нее
следует, что если несколько человек обменялись рукопожатиями, то общее
число пожатых рук обязательно четно, ибо в каждом рукопожатии участвуют
две руки (при этом каждая рука считается столько раз, сколько она
участвовала в рукопожатиях).
сумма степеней всех его вершин — число четное, равное
удвоенному числу ребер графа, так как каждое ребро участвует в этой сумме
ровно два раза. Этот результат, известный еще более двухсот лет назад Эйлеру,
часто называют леммой о рукопожатиях. Из нее
следует, что если несколько человек обменялись рукопожатиями, то общее
число пожатых рук обязательно четно, ибо в каждом рукопожатии участвуют
две руки (при этом каждая рука считается столько раз, сколько она
участвовала в рукопожатиях).
2. Количество нечетных вершин любого графа четно.
3. Во всяком графе с  вершинами, где
вершинами, где  ,
всегда найдутся по
меньшей мере две вершины с одинаковыми степенями.
,
всегда найдутся по
меньшей мере две вершины с одинаковыми степенями.
4. Если в графе с вершинами 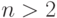 в точности две вершины имеют
одинаковую степень, то в этом графе всегда найдется либо в точности одна
вершина степени
в точности две вершины имеют
одинаковую степень, то в этом графе всегда найдется либо в точности одна
вершина степени  , либо в точности одна вершина
степени
, либо в точности одна вершина
степени  .
.

