Представления о планарном графе

Плоский граф

Плоским графом называется граф, изображенный на плоскости так, что никакие два его ребра (или, вернее, представляющие их кривые) геометрически не пересекаются нигде, кроме инцидентной им обоим вершины. Граф, изоморфный плоскому графу, называется планарным. Планарный граф можно определить еще так: граф планарен, если его можно уложить на плоскости. Рисунок графа, в котором никакие два его ребра не пересекаются, если не считать точками пересечения общие вершины, называют плоским представлением графа. Ясно, что плоское представление имеет только плоский граф. Обратно, у всякого плоского графа непременно найдется плоское представление. Плоские графы — это простые циклы, деревья, лес, а также граф, содержащий цикл, из вершин которого "выходят" деревья.

Пример. Примером неплоского графа может служить полный граф с пятью вершинами. Любые попытки начертить его плоское представление обернутся неудачей.

В качестве характеристики плоского представления графа вводится понятие грани. Гранью в плоском представлении графа называется часть плоскости, ограниченная простым циклом и не содержащая внутри других циклов.

Пример.

На рисунке показано плоское представление графа с тремя гранями: , , . Часть плоскости, ограниченная простым циклом , гранью не является, так как содержит цикл . Простой цикл, ограничивающий грань, называется границей грани. Две грани будем называть соседними, если их границы имеют хотя бы одно общее ребро.

Пример.

В данном графе часть плоскости, ограниченная простым циклом , является гранью, так как ребро , расположенное внутри грани, не образует цикла.

Не является гранью заштрихованная часть плоскости в данном примере, так как она содержит цикл, да к тому же эта часть плоскости не ограничена циклом. Ребро 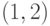является мостом, соединяющим циклы. Такие мосты называются перегородками.

В качестве грани можно рассматривать и часть плоскости, расположенную "вне" плоского представления графа. Она ограничена "изнутри" простым циклом и не содержит других циклов. Эту часть плоскости называют бесконечной гранью.

Пример.

На рисунке часть бесконечной грани заштрихована. Всякое плоское представление графа либо не имеет бесконечной грани, либо имеет в точности одну бесконечную грань. Как особый случай вводится бесконечная грань в плоском представлении дерева и леса. В плоском представлении дерева и леса за грань принимают всю плоскость рисунка.

Два графа гомеоморфны (или тождественны с точностью до вершин степени 2), если они оба могут быть получены из одного и того же графа "включением" в его ребра новых вершин степени 2.

Пример.

Изображенные графы гомеоморфны, и то же самое можно сказать о любых двух циклических графах. Гомеоморфность графов является отношением эквивалентности. Ясно, что введение термина "гомеоморфны" удобно только с технической точки зрения — включение или удаление вершин степени 2 не имеет никакого отношения к планарности. Добавление (включение) одной вершины, скажем , в какое-нибудь ребро, например , осуществляется следующим образом: пусть ребро инцидентно вершинам и . Тогда ребро удаляется из графа, но добавляются два новых ребра: 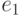инцидентное вершинам и , и 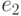, инцидентное вершинам и .

Введение понятия гомеоморфности графов позволяет установить следующий важный результат, известный как теорема Куратовского (точнее, как теорема Понтрягина-Куратовского, так как Л.С.Понтрягин доказал, но не опубликовал, эту теорему еще в 1927 году), которая дает необходимое и достаточное условие планарности графа.