Основные понятия теории графов

Связность графа

Назовем граф связным,если его нельзя представить в виде объединения двух графов, и несвязным — в противном случае.

Маршрутом в данном графе называется конечная последовательность ребер вида

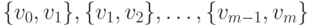
(обозначаемая также через 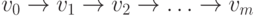). Очевидно следующее свойство маршрута: любые два последовательных ребра либо смежны, либо одинаковы. Но не всякая последовательность ребер, обладающая этим свойством, является маршрутом (в качестве примера рассмотрим звездный граф и возьмем его ребра в произвольном порядке). Каждому маршруту соответствует последовательность вершин 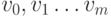. 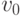называется начальной вершиной, а 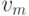конечной вершиной маршрута. Таким образом, мы будем говорить о маршруте из 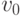в 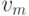. Заметим, что для любой вершины 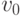тривиальным маршрутом, вообще не содержащим ребер, является маршрут из 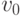в 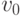. Длиной маршрута называется число ребер в нем. Маршрут называется цепью, если все его ребра различны, и простой цепью, если все вершины 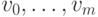различны, кроме, может быть, 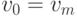. Замкнутая простая цепь, содержащая по крайней мере одно ребро, называется циклом. В частности, любая петля или любая пара кратных ребер образует цикл. Путь (последовательность ребер, ведущая от 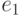к 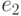, в которой каждые два соседних ребра имеют общую вершину и никакое ребро не встречается более одного раза) от вершины 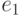до вершины 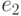называется простым, если он не проходит ни через одну из вершин графа более одного раза.

Граф называется связным, если для любых двух его вершин и существует простая цепь из в . Любой граф можно разбить на непересекающиеся связные графы, называемые компонентами ( связности ) графа . Таким образом, несвязный граф имеет, по крайней мере, две компоненты. Две вершины эквивалентны (или связаны ), если существует простая цепь из одной в другую.Связный граф состоит из одной компоненты. Граф называется несвязным, если число его компонент больше единицы.

Связный граф представляет собой простой цикл тогда и только тогда, когда каждая его вершина имеет степень .

Если 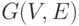— связный граф и степень каждой его вершины , тогда 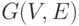— простой цикл.

Из каждой вершины данного графа в любую другую ведет путь. Начнем путь из какой-нибудь вершины е и пройдем по одному из двух ребер, которым принадлежит эта вершина. Попав во вторую вершину, выйдем из нее по второму ребру и так далее. С необходимостью все ребра графа будут пройдены, и мы вернемся в исходную вершину.

Если граф 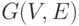— простой цикл, тогда степень каждой вершины равна двум.

Так как граф 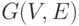— замкнутый простой путь, то из каждой его вершины можно попасть в любую другую, не проходя ни через одну вершину более одного раза. Степень каждой вершины такого графа равна двум.

Покажем, что в простом цикле не может быть вершины, степень которой не равна двум.

Если какая-то вершина в графе имеет степень меньше двух, то она не принадлежит никакому простому циклу.

Если какая-то вершина имеет степень больше двух, то никакой простой цикл (по определению) не может содержать все ребра, которым принадлежит эта вершина.