Алгоритмы сжатия изображений без потерь

13.6. Арифметическое кодирование

Классические статистические алгоритмы сопоставляют элементу кодируемой последовательности некий код. Алгоритмы арифметического кодирования кодируют сразу цепочку элементов в число-дробь 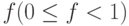[40]. При этом учитывается распределение вероятностей появления элементов в последовательности.

Пусть a₁, . . . , a_n - алфавит, все возможные одноэлементные цепочки; p₁, . . . , p_n - вероятности появления элементов (весов) ( p_j = Prob(a_j) ). Разобьем полуинтервал [0, 1) на n непересекающихся полуинтервалов I₁, . . . , I_n, соответствующих элементам a₁, . . . , a_n, причем длина I_j пропорциональна p_j.

Далее строится кодирующая дробь: производится построение системы вложенных полуинтервалов так, что каждый последующий полуинтервал занимает в предыдущем место, соответствующее положению элемента в исходном разбиении полуинтервала [0, 1).

Кратко процесс выглядит так:

• считывание очередного элемента;
• выбор соответствующего полуинтервала из разбиения текущего полуинтервала (на первом шаге - [0, 1) ).

По окончании этого процесса можно взять любое число из получившегося полуинтервала. Обычно число выбирают так, чтобы его запись в двоичном виде была самой короткой. Также часто накладывают ограничение на длину получившейся двоичной дроби. При превышении этого ограничения текущая дробь выводится, и начинается сначала формирование новой, дополняющей предыдущую(ие).

// elem - элемент
// in - вход, out - выход
// cleft - текущая левая граница полуинтервала
// cright - текущая правая граница полуинтервала
// interv - массив границ в исходном разбиении

cleft = 0;
cright = 1;
while( in.Read( elem ) ) // пока есть данные
{
     // длина текущего полуинтервала
     d = cright - cleft;
     // вычислим границы нового полуинтервала
     cright = cleft + d*interv[elem].right;
     cleft = cleft + d*interv[elem].left;
}
// ищем дробь внутри [left, right)
frac = Between( left, right );
out.Write( frac );

Сожмем следующую последовательность "TOBEORNOTTOBE".

• Составим таблицу весов:

  элемент алфавита	B	E	N	O	R	T
  вес	2	2	1	4	1	3
• Построим разбиение полуинтервала [0, 1):
  

  
  
  • На входе T, тогда правая граница полуинтервала будет , левая - 1, длина - ;
  • На входе O, тогда правая граница полуинтервала будет , левая - , длина - ;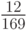
  • На входе B, тогда правая граница полуинтервала будет , левая - , длина - ;
  • На входе E, тогда правая граница полуинтервала будет , левая - , длина - ;
  • ...
  • На входе E, тогда правая граница полуинтервала будет , левая - , длина -
• Двоичную дробь можно взять такую: 0.1101110001010110000001000000101, т.к. двоичная запись границ итогового полуинтервала следующая: левая - 0.1101110001010110000001000000100111010011000101101, правая - 0.1101110001010110000001000000101101100100100100001.

Закодированная последовательность имеет длину 31 бит. Исходная, если считать алфавитом набор ASCII - 104 бита, если считать алфавитом только набор "TOBERN" - 39 бит.

Декодирование заключается в расшифровке дроби по известному распределению вероятностей появления элементов в последовательности. Следовательно, требуется хранить или передавать информацию о распределении вероятностей появления элементов. Для того чтобы обойти это требование, а также для того чтобы избавиться от необходимости совершать два прохода по последовательности, были предложены адаптивные модификации алгоритма.

// elem - элемент, in - вход, out - выход
// interv - массив границ в исходном разбиении
// frac - кодирующая дробь
// cleft - текущая левая граница полуинтервала
// cright - текущая правая граница полуинтервала
// nelem - количество элементов, закодированное дробью

i = nelem;
in.Read( frac );
while( i > 0 ) // пока надо декодировать
{
     // ищем элемент по дроби и разбиению полуинтервала
     elem = GetElem( interv, frac );
     out.Write( elem );
     // вычислим границы полуинтервала
     cright = interv[elem].right;
     cleft = interv[elem].left;
     // длина полуинтервала
     d = cright - cleft;
     // преобразуем дробь
     x = (x - cleft) / d;
     // отметим обработку очередного элемента
     i--;
}

Опишем идею адаптивной модификации. Изначально предполагается, что появление всех элементов равновероятно. По мере поступления новых элементов веса и разбиение полуинтервала корректируются. При декодировании также осуществляется коррекция после обработки очередного элемента.

Арифметическое кодирование является почти оптимальным видом кодирования, т.е. дает коды, почти равные длинам оптимальных кодов из теоремы Шеннона. Однако такая эффективность достигается за счет больших вычислительных затрат. Существуют модификации алгоритма, использующие только операции сдвига и сложения без деления и умножения для ускорения процесса кодирования. К сожалению, практически все такие модификации защищены патентами. Часть этих патентов уже имеют истекший срок действия, другая часть - нет. Таким образом, по мере истечения сроков патентов эффективные реализации модификаций алгоритма арифметического кодирования будут вытеснять алгоритм Хаффмена в сферах, где производительность не является критичным требованием.