Алгоритмы сжатия изображений без потерь

13.4. Словарные алгоритмы

Главная идея, лежащая в основе алгоритмов данного типа, заключается в том, что вместо кодирования только по одному элементу входящей последовательности производится кодирование цепочки элементов. При этом используется словарь цепочек (созданный по входной последовательности) для кодирования новых.

Алгоритм LZ77

Данный алгоритм (алгоритм LZ77^{4Назван по именам авторов Абрахама Лемпеля (Abraham Lempel) и Якоба Зива (Jacob Ziv). Опубликован в 1977 году.} ) был одним из первых, использующих словарь [55]. В качестве словаря используются N последних уже закодированных элементов последовательности. В процессе сжатия словарь-подпоследовательность перемещается ("скользит") по входящей последовательности. Цепочка элементов на выходе кодируется следующим образом: положение совпадающей части обрабатываемой цепочки элементов в словаре - смещение (относительно текущей позиции), длина, первый элемент, следующий за совпавшей частью цепочки. Длина цепочки совпадения ограничивается сверху числом n. Соответственно, задача состоит в нахождении наибольшей цепочки из словаря, совпадающей с обрабатываемой последовательностью. Если же совпадений нет, то записывается нулевое смещение, единичная длина и только первый элемент незакодированной последовательности - {0, 1, e}.

Описанная выше схема кодирования приводит к понятию скользящего окна (англ. sliding window), состоящего из двух частей:

1. подпоследовательность уже закодированных элементов длины N - словарь - буфер поиска (англ. search buffer );
2. подпоследовательность длины n из цепочки элементов, для которой будет произведена попытка поиска совпадения - буфер предварительного просмотра (англ. look-ahead buffer).

В терминах скользящего окна алгоритм сжатия описывается так: если e₁, . . . , e_i - уже закодированная подпоследовательность, то e_i-N+1, . . . , e_i - суть словарь или буфер поиска, а e_i+1, . . . , e_i+n - буфер предварительного просмотра. Аналогично, задача состоит в поиске наибольшей цепочки элементов из буфера предварительного просмотра, начиная с элемента e_i+1, совпадающей с цепочкой из буфера поиска - эта цепочка может начинаться с любого элемента 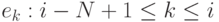и заканчиваться любым элементом 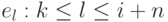, т.е. выходить за пределы буфера поиска, вторгаясь в буфер предварительного просмотра. Естественно, что выходить за пределы скользящего окна нельзя. Пусть в скользящем окне найдена максимальная по длине совпавшая цепочка элементов e_i-p, . . . , e_i+q, тогда она будет закодирована следующим образом: {p+1, q+p+1, e_i+p+q+2} - смещение относительно начала буфера предварительного просмотра (e_i+1), длина совпавшей цепочки, элемент, следующий за совпавшей цепочкой из буфера предварительного просмотра. Если в результате поиска найдено два совпадения с одинаковой длиной, то выбирается ближайшее к началу буфера предварительного просмотра. После этого скользящее окно смещается на p + q + 2 элементов вперед, и процедура поиска повторяется.

Выбор чисел N и n является отдельной важной проблемой, т.к. чем больше N и n, тем больше места требуется для хранения значений смещения и длины. Естественно, что время работы алгоритма также возрастает с ростом N и n. Отметим, что обычно N и n различаются на порядок.

Приведем пример сжатия данным алгоритмом. Сожмем строку "TOBEORNOTTOBE" с параметрами N = 10 и n = 3:

Если выделить для хранения смещения 4 бита, длины - 2 бита, а элементов - 8 бит, то длина закодированной последовательности (без учета обозначения конца последовательности) составит 4 x 8 + 2 x 8 + 8 x 8 = 112 бит, а исходной - 102 бита. В данном случае мы не сжали последовательность, а, наоборот, увеличили избыточность представления. Это связано с тем, что длина последовательности слишком мала для такого алгоритма. Но, например, рисунок кодового дерева Хаффмена на рис. 13.1, занимающий 420 килобайт дискового пространства, после сжатия имеет размер около 310 килобайт.

Ниже приведен псевдокод алгоритма сжатия.

// M - фиксированная граница
// считываем символы последовательно из входного потока
// in - вход - сжатая последовательность
// n - максимальная длина цепочки
// pos - положение в словаре, len - длина цепочки
// nelem - элемент за цепочкой, str - найденная цепочка
// in - вход, out - выход
// SlideWindow - буфер поиска
while( !in.EOF() ) //пока есть данные
{
     // ищем максимальное совпадение и его параметры
     SlideWindow.FindBestMatch( in, n, pos, len, nelem );
     // пишем выход: смещение, длина, элемент
     out.Write( pos );
     out.Write( len );
     out.Write( nelem );
     // сдвинем скользящее окно на len + 1 элементов
     SlideWindow.Move( in, len + 1 );
}

Декодирование сжатой последовательности является прямой расшифровкой записанных кодов: каждой записи сопоставляется цепочка из словаря и явно записанного элемента, после чего производится сдвиг словаря. Очевидно, что словарь воссоздается по мере работы алгоритма декодирования.

Видно, что процесс декодирования значительно проще с вычислительной точки зрения.

// n - максимальная длина цепочки
// pos - положение в словаре, len - длина цепочки
// nelem - элемент за цепочкой, str - найденная цепочка
// in - вход, out - выход
// Dict - словарь

while( !in.EOF() ) //пока есть данные
{
     in.Read( pos );
     in.Read( len );
     in.Read( nelem );
     if( pos == 0 )
     { //новый отдельный символ
          //удаляем из словаря первый (дальний) один элемент
          Dict.Remove( 1 );
          //добавляем в словарь элемент
          Dict.Add( nelem );
          out.Write( nelem );
     }
     else
     {
          //скопируем соответствующую строку из словаря
          str = Dict.Get( pos, len );
          //удалим из словаря len + 1 элементов
          Dict.Remove( len + 1 );
          //Добавляем в словарь цепочку
          Dict.Add( str + nelem );
          out.Write( str + nelem );
     }
}

Данный алгоритм является родоначальником целого семейства алгоритмов, и сам по себе в изначальном виде практически не используется. К его достоинствам можно отнести приличную степень сжатия на достаточно больших последовательностях, быструю распаковку, а также отсутствие патента^{5документ, обеспечивающий исключительное право эксплуатировать изобретение в течение известного времени (обычно 15-20 лет)} на алгоритм. К недостаткам относят медленную скорость сжатия, а также меньшую, чем у альтернативных алгоритмов, степень сжатия (модификации алгоритма борются с этим недостатком). Сочетание алгоритмов Хаффмена (Huffman) ( "Алгоритмы сжатия изображений без потерь" ) и LZ77 называют методом DEFLATE^{6Так называется сжатие, а разжатие называется INFLATE (англ. DEFLATE - сдувать, INFLATE - надувать).}. Метод DEFLATE используется в графическом формате PNG, а также в универсальном формате сжатия данных ZIP.