Выделение объекта на фоне
10.3. Алгоритм "Умные ножницы"
Алгоритм "умные ножницы" (англ. intellegent scissors), представленный в 1996 году, быстро завоевал популярность и был встроен в самый мощный и широко распространенный редактор фотоизображений Adobe Photoshop под именем "магнитное лассо" (англ. magnetic lasso). На первый взгляд, он близок к алгоритму, представленному нами как "нулевой вариант": при использовании "умных ножниц" пользователь обводит границу между объектом и фоном. Однако, в отличие от "нулевого варианта", пользователь не должен указывать все точки границы. Вместо этого он указывает точки на границе с некоторым промежутком, а "умные ножницы" проводят граничную линию между последовательно указанными точками.
Рассмотрим алгоритм проведения граничной линии от одной точки до другой, используемый "умными ножницами". Как и раньше, будем считать, что у нас есть изображение A с цветами пикселей A(x, y) и дана метрическая функция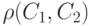 
, задающая расстояние между двумя цветами. Рассмотрим растровую решетку как граф, устроенный следующим образом. Вершинами графа служат углы пикселей, а ребрами графа - стороны пикселей. Будем считать, что пользователь в качестве последовательных граничных точек указал два угла пикселей, соответсвующих вершинам графа P и Q (рис. 10.2).
Рис. 10.2. Граф на растре (ребра нарисованы пунктиром). Пользователем заданы две вершины P и Q. Жирным выделен кратчайший путь на графе из P в Q, являющийся граничной линией между объектом и фоном.
Припишем каждому ребру длину1Эта длина будет отлична от геометрической длины стороны пикселя., обратно зависящую от разницы между цветами пикселей, которые примыкают к ребру. Например 
, где d - приписываемая длина ребра, L - геометрическая длина ребра, C1 и C2 - цвета пикселей по обе стороны от ребра, а K - некоторая константа. В качестве
граничной линии на участке между граничными точками P и Q "умные ножницы" выбирают кратчайший путь на графе, т.е. последовательность ребер, соединяющих вершины P и Q и имеющих минимальную суммарную длину. Поскольку ребра, соответствуюшие резким цветовым перепадам, имеют меньшую приписанную длину, "умные ножницы" стремятся провести границу именно по таким ребрам (рис. 10.2).
Рис. 10.3. Выделение объекта при помощи алгоритма "Умные ножницы". Вверху- процесс выделения. Квадратиками указаны граничные точки, заданные пользователем на данный момент. Внизу - результат выделения.
Мы не будем здесь рассматривать задачу поиска кратчайшего пути на графе. Данная задача является одной из основных задач дискретной математики, и соответствуюшие алгоритмы (например, алгоритм Дейкстры) приведены в большинстве учебников (см. например, [4] и [6]). Скажем лишь, что сложность данного алгоритма пропорциональна количеству вершин в графе.
Работа "умных ножниц" улучшается, если в рассмотренный граф добавить дополнительные ребра, например ребра, соответствующие диагоналям пикселей. Результат работы "умных ножниц" представлен на рис. 10.3. На левом рисунке показан процесс работы - пользователь добавляет точки по одной и в каждый момент времени ему показывается, как пройдет граница, если он поставит следующую граничную точку в месте расположения курсора. Справа показан результат работы. Он, очевидно, гораздо лучше результата, полученного при помощи "волшебной палочки". Во многих случаях "умные ножницы" существенно ускоряют процесс выделения объекта. Однако "умные ножницы" работают не очень хорошо при наличии пестрого фона и/или пестрого объекта (отсюда куски фона вокруг ног на рис. 10.3). В таких случаях "умные ножницы" требуют большого количества граничных точек, указанных пользователем, и выигрыш от их применения по сравнению с "нулевым вариантом" невелик.