Основные понятия последовательного анализа

Получение случайных выборок

Каждому из нас приходится иметь дело с ненадежными прогнозами погоды, с долговременными планами и прогнозами в промышленности и политике. Так как будущее нам сегодня не известно, исследование будущего (футурология) стоит перед вопросами о том, что может быть на переднем крае в интересующей нас области. На некоторых аспектах прогностики стоит коротко остановиться.

Распространение выводов, получаемых по выборке, на всю генеральную совокупность, используемое при предварительных расчетах результатов выборов, в официальной статистике, при изучении рынка или общественного мнения и тому подобное, называется предсказанием (Hochrechnung), так как при этом частота появления признака 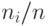, определенная по выборке, умножается на число элементов в генеральной совокупности и образует оценку 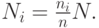Примерно так компьютер по немногим поступившим данным предсказывает результат выборов.

Долговременные прогнозы, или, лучше сказать, предварительные оценки, например, роста населения, потребления энергии, рынка рабочей силы, образуются на основе анализа тенденции развития; реже, но с большими предубеждениями и большими ошибками – на основании аналогии (и интуииции).

Среди немногих известных источников ошибок следует указать на неучет обратного влияния правильных, разумных предсказаний. Предсказанная в 1955 году в США резкая нехватка научных кадров в 1965-1970 годах не реализовалась. Число учащихся выросло скачком (вероятно, именно вследствие этой мрачной перспективы). Этот пример отчетливо показывает возможное влияние предварительных прогнозов.

Если необходимая для прогноза информация полностью или почти отсутствует, то пользуются методом опроса компетентных специалистов, методом экспертных оценок . Способ заключается в том, что экспертам выдается тщательно продуманная анкета. Слишком субъективные и необычные мнения можно исключить, сообщая участникам остальные ответы, чтобы каждый еще раз мог продумать свое мнение с учетом остальных. После нескольких подобных операций образуется общее мнение, которое может качественно превосходить каждое отдельное мнение.

Последовательные проверки статистических гипотез

В классической теории математической статистики объем выборки считается постоянным для каждой задачи. Существенным в последовательной проверке гипотез является то, что количество наблюдений, необходимых для принятия решения, зависит от исхода самих наблюдений и является случайной величиной. Сущность такой проверки состоит в следующем.

Пусть установлено некоторое правило, в соответствии с которым на каждом этапе эксперимента принимается одно из трех решений:

• принять гипотезу;
• отклонить гипотезу;
• продолжить эксперимент и провести дополнительное наблюдение.

Тогда после первого наблюдения проверка может быть закончена, если принято одно из первых решений, или производится второе наблюдение, если принято третье решение. На основе двух наблюдений опять принимается одно из трех решений и так далее, пока не будет принято первое или второе решение. Поясним это на примере выборочной проверки партии, состоящей из N однотипных изделий.

Предположим, что задано допустимое отношение числа негодных деталей 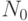к общему их количеству , то есть

( 12.1)

В результате выборочного контроля будет получено отношение

( 12.2)

где — число негодных изделий выборки;

— объем выборки (число испытаний).

Если бы отношение (12.2.) полностью соответствовало отношению (12.1.), то при вся партия была бы принята, а при 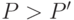— забракована.

Однако точное значение остается неизвестным, и это может привести к ошибке — существенной или несущественной. Для ее оценки устанавливаются границы отношения 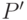, которые обозначаются через 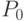и 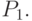Ошибка считается существенной и называется ошибкой первого рода, если партия бракуется при , или ошибкой второго рода, если принимаются при 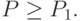Следовательно, сущность ошибки первого рода заключается в том, что бракуется партия при малом проценте брака, а сущность ошибки второго рода – что принимается партия при большом проценте брака.

Если задаться вероятностью совершить ошибку первого рода и вероятностью совершить ошибку второго рода, то вероятность забраковать партию при должна быть не больше , вероятность принять партию при 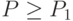не больше 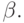Отсюда вероятность забраковать партию при 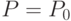будет равна , а вероятность принять партию при 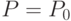равна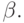

После проверки изделий, среди которых оказалось негодных и

годных изделий, можно определить вероятность получения такого результата по следующей формуле:

,

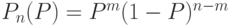где — вероятность того, что изделие не удовлетворяет требованиям.

Для граничных условий получим следующие выражения:

,

где — вероятность того, что ;

— вероятность того, что

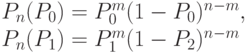Очевидно, что с увеличением 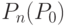и уменьшением 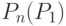возрастают основания для принятия партии, а с уменьшением 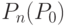и увеличением 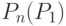возрастают основания забраковать партию. Поэтому в качестве критерия при последовательном анализе принимается отношение 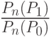, называемое коэффициентом правдоподобия.

Считается, что если 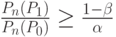, то партия бракуется, а если ,

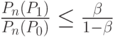то партия принимается. Значит, при

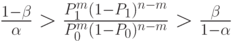( 12.3)

число экспериментов еще недостаточно и необходимо произвести наблюдений.

После логарифмирования и преобразования неравенства (12.3.) получается следующее неравенство

( 12.4)

где

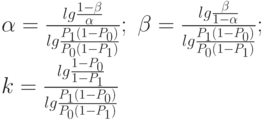( 12.5)

Следовательно, если удовлетворяет неравенству (12.4.), необходимо провести наблюдений; при 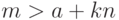партия бракуется, а при 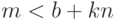партия принимается.

Рассмотренное правило последовательного анализа при приемочной проверке дает тем надежнее результат, чем ближе к единице вероятность принятия партии изделий при и ее отклонения при Для этого следует уменьшить величины и и разность Однако при этом увеличивается среднее ожидаемое число экспериментов, которое необходимо провести до получения определенного решения.

Пример.

Применение последовательного анализа при проверке целесообразности применения тактического приема (Динер И.Я. Исследование операций. Л. , ВМОЛУА, 1961).

При исследовании целесообразности использования в предполагаемых действиях некоторого тактического приема производится ряд испытаний (розыгрышей) планируемых действий с применением этого тактического приема. Хотя розыгрыши производятся в одних и тех же условиях, действия (в силу ряда случайных факторов) приводят к несовпадающим результатам. Тактический прием можно считать целесообразным, если (в данном примере) ему соответствует вероятность выполнения задачи , и нецелесообразным — при 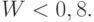Однако такое требование недостаточно для проведения последовательного анализа – необходимо определить нечувствительную зону и допускаемый риск, связанный с неправильным решением. Можно, например, потребовать, чтобы с вероятностью не больше 0,2 принималось решение о том, что тактический прием целесообразен при 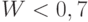, и с вероятностью не больше 0,3 принималось решение о том, что тактический прием нецелесообразен при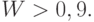

При этом будем иметь:

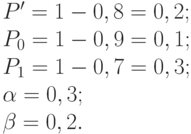
По формулам (12.5) находим для этого допуска:

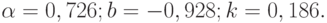
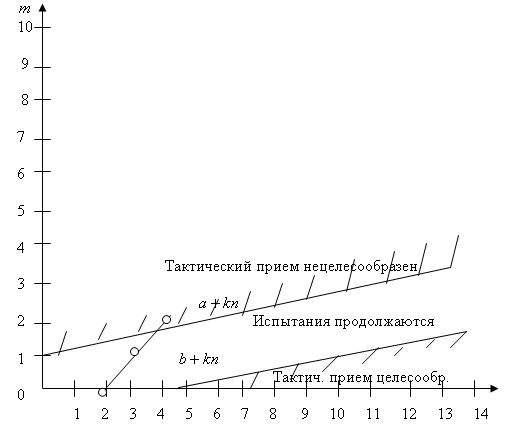
Графическое изображение критической области дано на рис. 12.1.

Рис. 12.1.

Последовательность выполнения и невыполнения планируемой задачи может быть изображена графически на том же рисунке, что и критическая область. Например, последовательности выполнения (+) и невыполнения (-) задачи 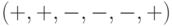соответствуют значения:

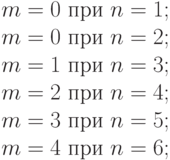
Нанеся эти точки на график, обнаруживаем, что после первого, второго и третьего розыгрышей они лежат внутри критической области, и, следовательно, необходимо продолжать испытания предлагаемого тактического приема. Однако после четвертого розыгрыша, давшего отрицательный результат, соответствующая точка 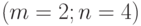выходит за пределы критической области, что позволяет в условиях принятого допуска прекратить дальнейшие испытания и отвергнуть предполагаемый тактический прием безотносительно к возможным результатам пятого и последующих розыгрышей. Заметим, что в условиях данного примера тактический прием был бы отвергнут после первого же розыгрыша, — он был бы принят, если бы первые пять розыгрышей подряд дали положительный результат.