Основные принципы математического моделирования

Определение моделирования

Моделированием называют построение модели того или иного явления реального мира. В общем виде модель — это абстракция реального явления, сохраняющая его существенную структуру таким образом, чтобы ее анализ дал возможность определить влияние одних сторон явления на другие или же на явления в целом. В зависимости от логических свойств и связей моделей с отображаемыми явлениями можно все модели разделить на три типа: изобразительные, аналоговые и математические.

Изобразительная модель отражает внешние характеристики явления и подобна оригиналу. Это наиболее простая и конкретная модель. Являясь в общем описательной моделью, она, как правило, не дает возможности установить причинные связи явления и соответственно определить или предсказать последствия изменений различных параметров явления. Характерная особенность такой модели – близкое совпадение ее свойств со свойствами отображаемого объекта. Эти свойства обычно подвергаются метрическому преобразованию, т.е. берется определенный масштаб.

В аналоговых моделях свойство данного явления отображается посредством свойств другого явления. Так, например, любая диаграмма представляет аналоговую модель некоторого явления. К аналоговым моделям относятся также морские карты, на которых совокупностью условных обозначений отображается совокупность свойств той или иной акватории. Преимущество аналоговой модели перед изобразительной состоит в том, что она позволяет отображать динамику явления. Другим преимуществом является большая универсальность этой модели: путем ее изменения можно отобразить различные процессы данного явления.

Математическая модель

Математическая модель является самой сложной и наиболее общей и абстрактной по сравнению с изобразительной и аналоговой. В ней для отображения свойств изучаемого явления используются символы математического или логического характера. Особые трудности возникают при решении задач с большой размерностью, расплывчатой постановкой, неопределенностью информации и т.д. В постановке таких задач появляются неклассические моменты, такие, как плохая формализуемость, нестандартность, противоречивость.

Остановимся на понятии плохо формализуемой задачи, которое появляется в результате решения потока серьезных прикладных задач в самых различных областях. Это могут быть и формализованные правила рассуждений, и правила логического вывода. Математические модели служат отражению и анализу некоторых свойств действительных объектов. Рассмотрим один из видов математических моделей, характеризующихся простой структурой и широко применяющихся в приложениях. Модели такого вида содержат следующие элементы:

1. вектор параметров, измеряемых на объекте: где — значение -го параметра, которое является чаще всего вещественным числом. Можно назвать вектором состояния объекта. Если изучается динамика моделируемого объекта во времени 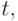то считается, что состояние в каждой момент описывается вектором ;
2. вектор 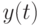параметров, которые не могут быть непосредственно измеренными;
3. неизвестные связи между переменными координатами векторов 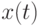и ;
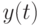4. связи между переменными, являющиеся неизвестными;
5. математический аппарат исследования соотношений (связей).

В качестве примера можно привести имитационные модели, описывающие возможные пути развития сложных технико-экономических и природных систем.

Плохо формализуемые задачи

Поясним теперь, что понимается под плохо формализуемыми задачами: это задачи, условия которых определены не полностью, не все связи заданы в аналитической форме, при этом формулировка задачи может содержать противоречия, а также не все соглашения о понятии решения могут быть в наличии.

Решению таких (плохо формализуемых) задач предшествуют этапы преобразования их формулировки, уточнений и упрощений. Результатом этих этапов является получение комплекса формализованных задач, имеющего некоторое отношение к исходной задаче. Необходимо знание этого отношения, иначе точность, достигаемая формальными методами, может оказаться бесполезной.

В сферу модели естественно также включить описание исходной задачи, выбираемый язык, критерии и ограничения, аппарат адекватности модели, средства интерпретации и подготовки к практическому внедрению, способы внемодельного анализа, учета плохо формализуемых факторов.

Можно выделить следующие разновидности плохо формализуемых задач.

1. Нестационарные — эти задачи отличаются эволюцией информации об объекте и модельных представлений о нем.
2. Задачи с расплывчатым отражением некоторых зависимостей и плохо определенными ограничениями. Здесь для описания зависимостей и ограничений требуется использовать специальные процедуры диалога с экспертами, а также проводить целенаправленные серии экспериментов.
3. Задачи с несовместными системами условий и ограничений и неопределенным понятием решения (неособенные задачи).
4. Задачи, в которых оценка решения производится по системе несогласованных (противоречивых) критериев.
5. Задачи с неоднозначно определенным решением.
6. Неустойчивые или некорректные задачи.

Противоречивые модели

Противоречивые знаковые модели возникают и в эмпирических исследованиях, и в формально-логических. Поэтому необходимо использовать обобщения понятия существования решения, применять "размытые" определения и принципы принятия практических решений, вводить обобщения понятия непротиворечивости теоретической модели. Так, например, некоторые логические парадоксы могут быть связаны с несовместными системами предикатов, которым можно поставить в соответствие лишь несобственные объекты. Один из путей снятия таких парадоксов — в расширении представлений об объектах, в ослаблении накладываемых при определении объекта требований, в их "размывании", в расширении смысла понятия существования объекта.

Противоречивые определения объектов и противоречивые модели иногда возникают в результате абсолютизации локальных свойств реально существующих объектов. Другая возможная причина появления противоречивых моделей — наличие различных несогласованных источников информации, которая служит основой моделирования.

В прикладной математике наблюдается заметный интерес к описанию противоречивых ситуаций; он вызван, вероятно, необходимостью повысить реальный результат применения математических моделей и методов к решению сложных практических задач. Примеры решения противоречивых задач можно видеть и в сфере оптимизации, и в сфере распознавания образов. В некоторых случаях содержательный смысл модели может диктовать такой вид работы с ней, как выделение ее непротиворечивых подмоделей, в других случаях возможно ослабление ограничений модели, приводящее к ее непротиворечивости.

Основы процесса выработки решений

В процессе выработки решений применимы такие конкретные методы, как анализ, синтез, индукция, дедукция, аналогия, абстракция и конкретизация.

Анализ – логический прием расчленения целого на отдельные элементы с рассмотрением каждого из них в отдельности. При этом в процессе выработки решения анализу подвергаются поставленная задача, данные обстановки.

Анализ неразрывно связан с синтезом — объединением всех данных, полученных в результате анализа. Синтез — это не простое суммирование результатов анализа. Задача его состоит в мысленном воспроизведении основных связей между элементами обстановки. Синтез дает возможность вскрыть сущность процессов, установить причинно-следственные связи, прогнозировать развитие действий.

Анализ и синтез тесно переплетаются с индукцией и дедукцией. Индукция — движение мысли от частного к общему, от ряда факторов к закону. Дедукция, наоборот, идет от общего к частному, от закона к отдельным его проявлениям. Индуктивный прием используется в тех случаях, когда на основе частного фактора можно сделать общие выводы, установить взаимосвязь между отдельными явлениями и каким-либо законом. Анализируя обстановку, необходимо следовать то от частного к общему (индукция), то от общего к частному (дедукция), стремясь установить взаимосвязь между явлениями обстановки и законом.

В процессе выработки решения можно использовать абстрагирование — способность отвлечься от совокупности факторов и сосредоточить внимание на каком-либо одном вопросе. При абстракции хотя и достигаются частные цели, однако они не могут служить основанием для решения. Поэтому наряду с абстракцией должна применяться конкретизация — увязка того или иного явления с конкретными условиями.

Существенное значение в процессе выработки решений может сыграть аналогия — прием, в котором из сходства двух явлений в одних условиях делается вывод о сходстве этих явлений в других условиях. Однако, аналогия — не доказательство, она лишь дает почву для высказывания предположения о возможном развитии характера действий, дает толчок в мышлении.

В ходе выработки решения важно установить причинно-следственные связи между элементами. Причинность — одна из всеобщих форм объективной связи между предметами, явлениями и процессами реальной действительности.