|
мне задали дистанционное задание на сертификат,но я не могу его найти |
Метод вычисления оптимальных стратегий
Введение
Квазиматричные игры относятся к некоторому специальному классу позиционных антагонистических игр двух лиц со случайным ходом.
Игроками I и II, как и в матричных играх, являются противники, преследующие прямо противоположные цели и имеющие конечное число возможных вариантов действий. Случайный ход делает " природа ", которая, не преследуя какой-либо цели (в силу объективных факторов, независимых от воли игроков), выбирает из конечного множества одну альтернативу. Такой выбор представляет собой случайный ход . Наличие "природы" как третьего игрока приводит теоретико-игровую задачу к классу позиционных игр, так как в этом случае число последовательных ходов будет всегда более двух. При этом если оба игрока не знают, какой ход сделает "природа", то такая игра в нормальной форме является матричной игрой. Однако анализ конфликтных ситуаций, моделью которых является конечные игры, показывает, что в целом ряде случаев стороны имеют различную информацию о ходах "природы". Так, например, I может знать, а игрок II — не знать, какой ход сделает "природа". Такие игры и называются квазиматричными .
Описание квазиматричной игры
Правила квазиматричной игры формулируются следующим образом.
Пусть функция выигрыша игрока I задана множеством матриц
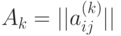
для 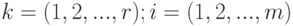 и
и 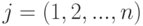 , где
, где  и
и  — альтернативы "природы", игрока I и игрока II соответственно.
— альтернативы "природы", игрока I и игрока II соответственно.
Из множества альтернатив "природы" случайным образом выбирается число  , которое сообщается только игроку I. Последний, зная матрицу
, которое сообщается только игроку I. Последний, зная матрицу  , выбирает число
, выбирает число  . В отличие от него игрок II должен выбрать число
. В отличие от него игрок II должен выбрать число  , зная только множество
, зная только множество  и распределение вероятности
и распределение вероятности 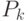 , в соответствии с которым выбирается число
, в соответствии с которым выбирается число  . В связи с этим игрок II не может применить свою оптимальную стратегию, которая вычисляется в зависимости от
. В связи с этим игрок II не может применить свою оптимальную стратегию, которая вычисляется в зависимости от  .
.
Игрок I, зная последнее обстоятельство, может использовать его в своих интересах и увеличить выигрыш. Игроку II тогда остается только не дать игроку I увеличить выигрыш более, чем это обусловлено разными объемами информации о функции выигрыша.
Для осуществления наилучшим образом своих интересов в квазиматричной игре игроки должны стремиться к ситуациям равновесия, то есть придерживаться своих оптимальных стратегий. Тогда значением квазиматричной игры 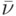 будет тот наибольший выигрыш, который игрок I может себе обеспечить (или, что то же самое, те наибольшие потери игрока II, которые он вынужден понести), если каждый из них придерживается своей оптимальной стратегии.
будет тот наибольший выигрыш, который игрок I может себе обеспечить (или, что то же самое, те наибольшие потери игрока II, которые он вынужден понести), если каждый из них придерживается своей оптимальной стратегии.
Решение квазиматричных игр
Пусть игрок II знает априорные вероятности 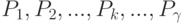 появления значений функций выигрыша:
появления значений функций выигрыша:
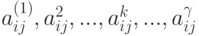 .
.
Чтобы найти оптимальные стратегии и значение игры, представим ее как трехходовую позиционную игру с неполной информацией. Развитие такой игры во времени, как известно, представляется как ряд последовательных этапов, на каждом из которых соответствующий игрок делает ход.
В квазиматричной игре на первом этапе делает ход "природа", которую обозначают числом 0. Следовательно, начальным узлом дерева будет кружок с числом 0 и информационным множеством 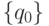 , состоящим из одного элемента
, состоящим из одного элемента  .
.
Из начального узла проводится s отрезков, каждый из которых соответствует матрице 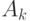 с вероятностью
с вероятностью 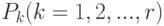 . На втором этапе делает ход игрок, имеющий полный объем информации. Следовательно, в каждой точке разветвления дерева на втором этапе имеется одно информационное множество
. На втором этапе делает ход игрок, имеющий полный объем информации. Следовательно, в каждой точке разветвления дерева на втором этапе имеется одно информационное множество 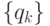 , состоящее из одного элемента
, состоящее из одного элемента  . Из каждого узла второго этапа проводится m отрезков, каждый из которых соответствует
. Из каждого узла второго этапа проводится m отрезков, каждый из которых соответствует  -ому ходу игрока, имеющего полный объем информации. Выбор этого игрока приводит к ситуации второго этапа, на котором делает ход игрок, имеющий неполный объем информации (он не знает, какой ход сделан на первом и втором этапах). Следовательно, этот игрок имеет только одно информационное множество, включающее все узлы третьего этапа. Выбор хода на третьем этапе приводит к одной из заключительных ситуаций, когда функция выигрыша принимает значение
-ому ходу игрока, имеющего полный объем информации. Выбор этого игрока приводит к ситуации второго этапа, на котором делает ход игрок, имеющий неполный объем информации (он не знает, какой ход сделан на первом и втором этапах). Следовательно, этот игрок имеет только одно информационное множество, включающее все узлы третьего этапа. Выбор хода на третьем этапе приводит к одной из заключительных ситуаций, когда функция выигрыша принимает значение 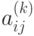 , если игра закончится в
, если игра закончится в  - вершине. Эту функцию выигрыша называют функцией выигрыша партии, так как она определяет выигрыш игрока I для конкретной партии.
- вершине. Эту функцию выигрыша называют функцией выигрыша партии, так как она определяет выигрыш игрока I для конкретной партии.
Стратегия игрока, как известно, должна указывать, что ему нужно делать на каждом этапе при любой возможной информации о сделанных ходах на всех предыдущих этапах.
Игрок I имеет полную информацию о ходах "природы". Поэтому его стратегия должна определять, какой отрезок дерева игры выбирается в  -м узле. Например, одной из стратегий игрока I является выбор в каждом узле отрезка 1. Другая стратегия игрока – выбор отрезка с наибольшим номером, то есть отрезка
-м узле. Например, одной из стратегий игрока I является выбор в каждом узле отрезка 1. Другая стратегия игрока – выбор отрезка с наибольшим номером, то есть отрезка  , и так далее. Поскольку у игрока I имеется r различных информационных множеств, которые имеют номера
, и так далее. Поскольку у игрока I имеется r различных информационных множеств, которые имеют номера  , то любую стратегию игрока I можно изобразить набором
, то любую стратегию игрока I можно изобразить набором  различных информационных множеств, которые имеют номера
различных информационных множеств, которые имеют номера  , то любую стратегию игрока I можно изобразить набором
, то любую стратегию игрока I можно изобразить набором  чисел, где
чисел, где  -е число изображает отрезок, выбранный, когда партия достигает
-е число изображает отрезок, выбранный, когда партия достигает  -го информационного множества. Таким образом, наборы из
-го информационного множества. Таким образом, наборы из  целых чисел
целых чисел
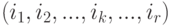
изображают стратегию игрока I. Например, стратегия, при которой всегда выбирается отрезок 1, изображается как
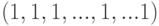 .
.
Обозначим множество стратегий игрока I через 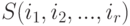 . Можно установить, что
. Можно установить, что 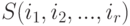 — функция, указывающая игроку I выбор числа
— функция, указывающая игроку I выбор числа  в зависимости от выбранного числа
в зависимости от выбранного числа  на первом этапе. Так, например, стратегия
на первом этапе. Так, например, стратегия 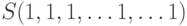 состоит в том, чтобы выбрать ход 1 независимо от того, какой ход сделан на первом этапе. Другая возможность стратегия
состоит в том, чтобы выбрать ход 1 независимо от того, какой ход сделан на первом этапе. Другая возможность стратегия 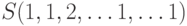 определяет выбор хода 2, если на первом этапе сделан ход 3, и хода 1 во всех остальных случаях.
определяет выбор хода 2, если на первом этапе сделан ход 3, и хода 1 во всех остальных случаях.
Игрок II, делающий ход на третьем этапе, не имеет информации о сделанных ходах на первом и втором этапах, поэтому его стратегия определяет только выбор числа  . Следовательно, множество стратегий этого игрока запись следующим образом:
. Следовательно, множество стратегий этого игрока запись следующим образом:
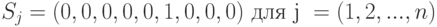 .
.
На основании изложенного видно, что стратегией игрока является функция, которая определена для каждого информационного множества, соответствующего игроку. Значение стратегии для каждого такого информационного множества представляет один из возможных ходов, имеющихся у игрока. Следовательно, число стратегий игрока будет определяться числом его информационных множеств и возможных ходов. Для игрока, имеющего полный объем информации, оно будет равно 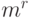 (поскольку
(поскольку  пробегает m значений и имеется
пробегает m значений и имеется  значений числа
значений числа  ), а для игрока, не имеющего информации о сделанных ходах на предыдущих этапах, будет равно
), а для игрока, не имеющего информации о сделанных ходах на предыдущих этапах, будет равно  .
.
Каждая пара стратегий  определяет математическое ожидание функции выигрыша
определяет математическое ожидание функции выигрыша 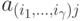 позиционной игры с неполной информацией:
позиционной игры с неполной информацией:
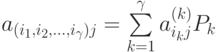 |
( 8.1) |
Вычисление  дает возможность составить нормализованную форму позиционной квазиматричной игры
дает возможность составить нормализованную форму позиционной квазиматричной игры 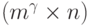 матрицу
матрицу
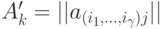 .
.
Решение игры, матрица которой равна  определяет оптимальные смешанные (в общем случае) стратегии
определяет оптимальные смешанные (в общем случае) стратегии  и
и  игроков I и II соответственно, а также значение игры
игроков I и II соответственно, а также значение игры 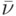 .
.
Очевидно, что вектор оптимальной смешанной стратегии игрока I можно записать следующим образом:
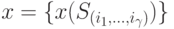 ,
,
где  — вероятность применения
— вероятность применения 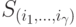 чистой стратегии. Тогда вектор оптимальной смешанной стратегии игрока II будет
чистой стратегии. Тогда вектор оптимальной смешанной стратегии игрока II будет
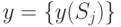 ,
,
где 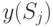 — вероятность применения
— вероятность применения 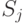 чистой стратегии. Соответственно значение игры
чистой стратегии. Соответственно значение игры 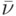 будет равно
будет равно
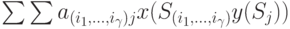 |
( 8.2) |
Однако найденное решение 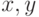 , по крайней мере для игрока I, еще не является решением квазиматричной игры. Действительно, смешанная стратегия
, по крайней мере для игрока I, еще не является решением квазиматричной игры. Действительно, смешанная стратегия  определяет лишь распределение вероятностей чистых стратегий игрока I в позиционной игре, и не более. В связи с этим воспользуемся понятием стратегия поведения.
определяет лишь распределение вероятностей чистых стратегий игрока I в позиционной игре, и не более. В связи с этим воспользуемся понятием стратегия поведения.
Под стратегией поведения игрока понимается распределение вероятностей по альтернативам, определенное для каждого его информационного множества.
Можно представить себе каждую чистую стратегию как книжку инструкций, в которой каждая страница относится лишь к одному информационному множеству и точно устанавливает, что нужно делать в этом информационном множестве. Множество стратегий соответствует библиотеке таких книг. Смешанная стратегия выбирает одну книгу из библиотеки посредством случайного механизма с распределением вероятностей, совпадающим с распределением вероятностей смешанной стратегии. Стратегия поведения представляет книгу другого рода, хотя каждая страница также относится к одному информационному множеству, она устанавливает распределение вероятностей по альтернативам этого множества, а не конкретный выбор (Н.Н. Воробьев. Бесконечные антагонистические игры//М., Изд-во физико-математической литературы, 1967. С.300).
В широком смысле стратегия поведения данного игрока есть функция, определенная на классе его информационных множеств, которая назначает для каждого информационного множества распределение вероятностей альтернатив этого множества. Очевидно, что если у игрока имеется только одно информационное множество, то его стратегия поведения такая же, как и смешанная. Если у игрока имеется более одного информационного множества, то каждая его смешанная стратегия задает ему единственную стратегию поведения, а именно соответствующее распределение вероятностей в каждом информационном множестве.
Как показал Г. Кун (Позиционные игры//Сб. под ред. Н.Н. Воробьева, М. "Наука" , 1987. ), для игр с полной памятью, а квазиматричные игры являются таковыми, всякая смешанная стратегия эквивалентна некоторой стратегии поведения. Следовательно, в квазиматричных играх всегда существует оптимальная стратегия поведения.
Метод вычисления оптимальных стратегий в квазиматричных играх реализованы в .NET на языке программирования C# (Институт вычислительной математики и математической геофизики СО РАН).
Применение метода : экономика;
военное дело.
