|
мне задали дистанционное задание на сертификат,но я не могу его найти |
Основные понятия последовательного анализа
Критерий Вальда
Для каждого из описанных ниже критериев будем предполагать, что необходимо выбрать одно из действий 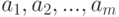 при выборе "природой" одного из состояний
при выборе "природой" одного из состояний  , в результате чего достигается выигрыш
, в результате чего достигается выигрыш 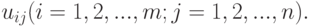
Критерий Вальда или максиминный критерий. В соответствии с этим критерием каждое действие оценивается по наихудшему для него состоянию, и оптимальным является действие, приводящее к наилучшему из наихудших состояний, то есть действие  , для которого достигается
, для которого достигается
 ,
,
Можно установить, что согласно максиминному критерию складывающаяся ситуация рассматривается как матричная игра и максиминная стратегия представляет собой наилучший выбор против минимаксной стратегии "природы", то есть против наименее благоприятного априорного распределения вероятностей состояний "природы". С этой точки зрения максиминный критерий является чрезвычайно консервативным, так как "природа" не представляет собой сколько-нибудь разумного игрока. Однако применение этого критерия может быть целесообразным, если по условиям обстановки подобный консерватизм имеет смысл.
Критерий минимаксного риска
Минимаксный критерий ( критерий потерь или минимаксного риска ). В соответствии с этим критерием оптимальным считается действие, для которого величина потерь (риска) принимает наименьшее значение при самой неблагоприятной обстановке, то есть действие  , для которого достигается
, для которого достигается
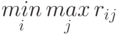 ,
,
где 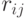 определяется как величина, которую нужно прибавить к
определяется как величина, которую нужно прибавить к  , чтобы получить максимальный выигрыш, состоящий в
, чтобы получить максимальный выигрыш, состоящий в  -м столбце.
-м столбце.
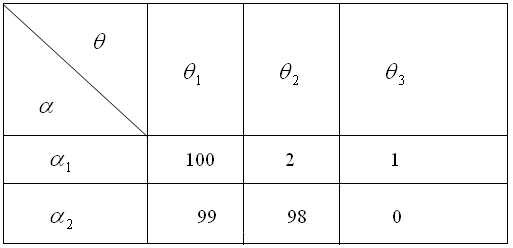
Для определения оптимального действия согласно минимаксному критерию на основании первоначальной матрицы выигрышей составляется вторая матрица, показывающая потери от ошибок (матрица потерь). Покажем составление матрицы потерь на конкретном примере.
Пусть матрица выигрышей задана таблицей на рисунке 12.a. Из рисунка 12.a видно, что если применяется действие  , а состояние "природы"
, а состояние "природы" 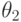 , то по отношению к действию
, то по отношению к действию  достигается наибольший выигрыш, равный 98 единицам, и, следовательно, игрок не несет никаких потерь. Поэтому показатель потерь на пересечении строки
достигается наибольший выигрыш, равный 98 единицам, и, следовательно, игрок не несет никаких потерь. Поэтому показатель потерь на пересечении строки  и столбца
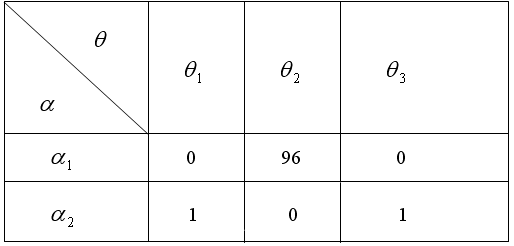
и столбца 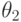 равен нулю. Этот показатель и записывается как элемент матрицы потерь. (См. рисунок 12.b) Если же игрок применяет действие
равен нулю. Этот показатель и записывается как элемент матрицы потерь. (См. рисунок 12.b) Если же игрок применяет действие  против стратегии
против стратегии 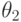 , то он получает только две единицы, тогда как максимально возможный выигрыш равен 98. Следовательно, показатель потерь в этом случае будет равен
, то он получает только две единицы, тогда как максимально возможный выигрыш равен 98. Следовательно, показатель потерь в этом случае будет равен  ; он записывается в таблицу на рисунке 12.b на пересечении строки
; он записывается в таблицу на рисунке 12.b на пересечении строки  и столбца
и столбца 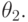 Остальные элементы матрицы потерь находятся аналогичным образом.
Остальные элементы матрицы потерь находятся аналогичным образом.
Критерий Гурвица
Критерий пессимизма-оптимизма. В соответствии с этим критерием оптимальным считается действие  , для которого достигается
, для которого достигается
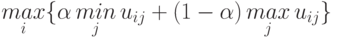 ,
,
где 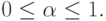
Из приведенного условия видно, что критерий Гурвица является взвешенной средней из наименьших и наибольших выигрышей для принятого коэффициента  В частности, при
В частности, при 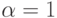 критерий Гурвица соответствует критерию Вальда. Заметим, что минимальный критерий учитывает только наибольший выигрыш, получаемый в результате применения любой стратегии, и безразличен к любым другим вариантам.
критерий Гурвица соответствует критерию Вальда. Заметим, что минимальный критерий учитывает только наибольший выигрыш, получаемый в результате применения любой стратегии, и безразличен к любым другим вариантам.
Критерий Лапласа
В соответствии с этим критерием оптимальным считается действие, которому соответствует
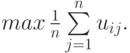
Следовательно, критерий Байеса (Лапласа) исходит из того, что раз совершенно неизвестно, какое из состояний  имеет место, то нужно поступить так, как будто они равновероятны.
имеет место, то нужно поступить так, как будто они равновероятны.
Последовательный анализ
Для построения математических (описательных и нормативных) моделей , как правило, бывает необходимо предварительно определить характеристики тех или иных случайных величин или вероятностей элементарных событий. Обычным путем определения подобных величин является обработка результатов наблюдений и измерений. Обработка таких результатов осуществляется методами математической статистики.
Особое значение для применения методов математической статистики имеет вопрос о числе наблюдений, полученных для оценки того или иного параметра. Классические методы статистики исходят из наличия, в крайнем случае, достаточного числа наблюдений. Однако в силу целого ряда причин не всегда возможно набрать необходимое число наблюдений. Достаточно указать, что увеличение числа наблюдений, как правило, ведет к увеличению затрат материальных средств и времени на проведение соответствующих испытаний. В подобных случаях число наблюдений целесообразно заранее не определять, а решение об окончании эксперимента принимать последовательно на каждом его этапе в зависимости от результатов предыдущих наблюдений, — иными словами, каждый последующий опыт производить лишь после того, как анализ полученных до него результатов покажет необходимость продолжения опытов. Такое направление в математической статистике, создателем которой является А. Вальд, получило название последовательного анализа . (А. Вальд. Последовательный анализ. М., Физматгиз, 1960.)
В последовательном анализе объем выборки не устанавливается заранее, а определяется в процессе анализа статистических данных, получаемых последовательно в порядке их поступления. Основное достоинство этого метода по сравнению с методами классической статистики в том, что он требует в среднем значительно меньшее число наблюдений.
Статистическая гипотеза
Статистической гипотезой называется предположение относительно величины параметров, входящих в распределение случайной величины. Решение о принятии или отклонении статистической гипотезы (далее будем говорить просто гипотезы) всегда принимается на основе конечного числа наблюдений. Совокупность конечного числа наблюдений называется выборкой . Количество наблюдений, составляющих выборку, называется объемом выборки .
Последовательные наблюдения  величины
величины  называются статистически независимыми, если условное распределение вероятностей
называются статистически независимыми, если условное распределение вероятностей  -го наблюдения
-го наблюдения 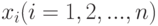 не зависит от величин предыдущих наблюдений. Будем рассматривать только случай, когда последовательные наблюдения
не зависит от величин предыдущих наблюдений. Будем рассматривать только случай, когда последовательные наблюдения  независимы в вероятностном смысле.
независимы в вероятностном смысле.