Типы систем массового обслуживания и критерии эффективности

Типы систем массового обслуживания

Протекание процесса обслуживания во всех случаях одинаковое – поток требований поступает и обслуживается системой обслуживания. Однако это сходство обнаруживается только в самых общих чертах. Каждой системе свойственна определенная организация. В соответствии с организацией определяется и характер задач массового обслуживания. Поэтому дальнейшие рассуждения о типах задач основаны прежде всего на отличиях, присущих той или иной организации обслуживающей системы. В настоящей лекции мы постараемся выделить основные типы задач и указать главные критерии, характеризующие протекание процесса.

Первым признаком, позволяющим разбить задачи массового обслуживания на группы, является поведение требования, поступившего в систему в момент, когда все обслуживающие аппараты заняты.

Первая группа задач характеризуется тем, что требование не может ждать начала обслуживания или, что фактически то же самое, система обслуживания отказывает требованию, поступившему в тот момент, когда все обслуживающие аппараты заняты. Ясно, что подобное свойство может иметь место только в системах с ограниченным числом обслуживающих аппаратов. Это свойство означает, что полностью отсутствуют условия для образования очереди. Если требование, поступившее в систему, получило отказ, то, следовательно, оно покидает систему не обслуженным. Оно потеряно для обслуживания в этой системе. Поэтому часто подобные обслуживающие системы называются системами с потерями , а соответствующие задачи массового обслуживания – задачами обслуживания в системах с потерями .

Вторая группа задач характеризуется тем, что требование, поступившее в систему обслуживания, может ее покинуть только тогда, когда оно полностью обслужено. Требований, ожидающих обслуживания, может оказаться довольно много. В этом случае все требования, поступившие в систему в тот момент, когда все обслуживающие аппараты заняты, образуют очередь. Поэтому такие системы обслуживания получили название систем с ожиданием , или систем без потерь. Соответствующие задачи массового обслуживания называются задачами в системах с ожиданием . Примерами систем обслуживания без потерь являются системы обслуживания самолетов при посадке на аэродром (здесь потеря требования равносильна гибели самолета).

Для задач третьей группы характерно наличие некоторых промежуточных условий.

Требование, поступившее в систему обслуживания в момент, когда все обслуживающие аппараты заняты, не обязательно должно покинуть систему, но и не обязательно будет ждать конца обслуживания. Оно покинет систему, если будут выполнены некоторые дополнительные условия. При этом в различных задачах условия, при которых требование должно покинуть обслуживающую систему, могут быть самыми разнообразными. Так, например, в некоторых задачах массового обслуживания таким условием является ограниченное время пребывания требования в системе обслуживания. Если суммарное время пребывания требования в системе обслуживания (которое складывается из времени ожидания начала обслуживания и времени обслуживания) превысит определенную величину, то требование покидает обслуживающую систему независимо от того, начато его обслуживание или нет; а если обслуживание начато — то независимо от того, закончено оно или нет.

Другим примером условий может быть ограничение времени ожидания начала обслуживания. Если время ожидания очередным требованием начала обслуживания превзойдет определенную величину, то требование покинет обслуживающую систему, но если обслуживание начато, то оно будет закончено независимо от того, какое время нужно затратить на его обслуживание.

Такого рода системы называются смешанными системами обслуживания, чем подчеркивается их промежуточное положение между системами с потерями и системами с ожиданием.

Кроме того, задачи различаются по числу обслуживающих аппаратов в системе. По этому признаку они могут быть разбиты на два типа: задачи обслуживания в системах с ограниченным числом обслуживающих аппаратов и задачи обслуживания в системах с неограниченным числом обслуживающих аппаратов.

Ясно, что реально неограниченного числа обслуживающих аппаратов ни в одной системе быть не может, однако могут быть системы, в которых число обслуживающих аппаратов настолько велико, что их можно относить к системам с неограниченным числом обслуживающих аппаратов. При очень большом количестве обслуживающих аппаратов ряд задач может быть с достаточной точностью и гораздо проще решен, если рассматривать эту систему как систему с неограниченным числом обслуживающих аппаратов.

Задачи массового обслуживания различаются еще по одному признаку – по числу требований, которые могут одновременно находиться в обслуживающей системе. В некоторых задачах число таких требований принципиально не может быть больше определенного числа. Это задачи с ограниченным числом требований.

В ряде задач число требований, находящихся одновременно на обслуживании, может быть очень большим. Настолько большим, что практически можно и удобно рассматривать поток требований как неограниченный. Здесь под словом "удобно" мы понимаем метод вычислений, а слово "можно" означает, что степень точности вычислений при этом будет достаточной для практического использования получаемого результата.

Рассматривать поток требований как неограниченный удобно также в тех случаях, когда заранее нельзя предопределить, насколько большое число требований может поступить.

Укажем еще на один признак, по которому различаются обслуживающие системы. Если аппараты обслуживающей системы расположены последовательно (пронумерованы) и очередное требование поступает сначала на первый из них и лишь только в том случае, если он занят, передается второму аппарату, и так далее, то, следуя А.Я.Хинчину, такую систему будем называть упорядоченной . Следовательно, в упорядоченной системе требование поступит на обслуживающий аппарат с номером только в том случае, если в момент его поступления аппараты с номерами 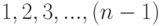заняты.

Критерии эффективности

При решении задач, связанных с массовым обслуживанием, большое значение имеет правильный выбор критериев, определяющих изучаемый процесс. Одна и та же система обслуживания может характеризоваться с различных точек зрения различными критериями эффективности. Выбор того или иного критерия должен производиться в каждом конкретном случае исходя из тех задач, которые ставятся перед системой. Перечислить все критерии, которые могут или могли бы быть полезными во всех задачах массового обслуживания, затруднительно, поэтому ограничимся наиболее существенными и наиболее часто используемыми.

Критерии эффективности систем обслуживания с потерями

1. Вероятность отказа равна вероятности того, что все обслуживающие аппараты окажутся занятыми. Вероятность отказа определяет, в какой степени данная система обслуживания способна удовлетворить поступающий поток требований. Этот критерий (вероятность отказа) не связан с качеством обслуживания внутри системы тех требований, которые были приняты на обслуживание. Он дает только внешнюю оценку способности системы приступить к обслуживанию поступившего требования.
2. Степень загрузки обслуживающей системы может характеризоваться таким критерием, как среднее число занятых аппаратов.
3. Более полно загрузка системы может характеризоваться законом распределения количества занятых аппаратов.
4. Может быть полезен такой критерий, как среднее количество потерянных требований за определенный промежуток времени.

Критерии эффективности систем обслуживания без потерь

Длина очереди является случайной величиной. В качестве характеристики длины очереди можно использовать ее математическое ожидание. Перечень критериев:

1. Математическое ожидание длины очереди.
2. Время ожидания начала обслуживания.
3. Закон распределения начала обслуживания (закон распределения времени ожидания удается найти не всегда, в этих случаях приходится пользоваться более простыми критериями).
4. Средняя длина очереди, полная характеристика которой может быть задана законом распределения длины очереди.
5. Среднее число занятых обслуживающих аппаратов (это число – величина случайная).
6. Вероятность иметь более m единиц в очереди в момент при заданном начальном состоянии системы.

Критерии эффективности системы обслуживания смешанного типа

Критерии, характеризующие протекание процесса обслуживания в системах смешанного типа, в основном совпадают с теми, которые были перечислены для задач первой и второй групп. Особые критерии для обслуживания систем смешанного типа таковы:

1. Время, затраченное на обслуживание тех требований, которые покинут систему до окончания обслуживания.
2. Суммарное время, затраченное всеми аппаратами системы.

Частные критерии в зависимости от специфики изучаемых конкретных процессов могут быть получены из этих основных с учетом особенностей каждого процесса

Задача 1.

Оценки параметров загруженности линий связи на междугородних телефонных станциях и линиях провайдеров. Аннотация

В данной задаче рассматриваются основные принципы для оценки параметров загруженности линий связи на междугородних телефонных станциях и линиях провайдеров при предоставлении услуг телекоммуникаций как инструмента аналитического анализа выгодности использования данного числа линий, а также для выработки стратегии экономической политики по представлению услуг связи. Предлагается аналитический аппарат и реализация математического обеспечения. Задачу обслуживания линий связи можно рассматривать как ситуацию, когда появляется необходимость в обслуживании требований (телефонных разговоров или сеансов доступа к сети Internet), поступающих в систему. Система телекоммуникаций приводит к образованию очереди, обладает ограниченными возможностями для удовлетворения запросов клиентов, что приводит к образованию очереди. Основной задачей организации, предоставляющей услуги телекоммуникации, является сокращение (в идеале — ликвидация) таких очередей при полной загрузке линий связи с целью их экономичного использования, ведь их техническая эксплуатация требует материальных вложений. Поэтому достаточно сложную задачу, имеющую множество ограничений, как со стороны уменьшения отказа в обслуживании, так и в полной загрузке линии, можно решать только комплексно. Задача анализа линий связи на междугородной автоматической станции или линий связи с провайдером доступа к сети Internet относится к задачам теории массового обслуживания. Общей особенностью таких задач является случайный характер исследуемых явлений (сеансы связи), так как количество требований на обслуживание, временные интервалы между их поступлениями и длительность обслуживания случайны. Основные элементы исследуемой системы следующие: входящий поток требований, который лучше всего реализовать с использованием систем управления базами данных, линии связи, очередь требований, которую можно представить в виде реестров предоставляемых услуг телекоммуникаций за отчетный период. Данная система относится к системе с потерями, так как всякое вновь поступившее требование, застав все линии связи занятыми, покидает систему.

Критерии эффективности

Максиминный критерий (критерий Вальда). В соответствии с этим критерием каждое действие оценивается по наихудшему для него состоянию, и оптимальным является действие, приводящее к наилучшему из наихудших состояний, то есть действие , для которого достигается

.

Минимаксный критерий (критерий потерь или минимаксного риска). В соответствии с этим критерием оптимальным считается действие, для которого величина потерь (риска) принимает наименьшее значение при самой неблагоприятной обстановке, то есть действие , для которого достигается

,

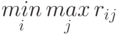где 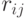определяется как величина, которую нужно прибавить к , чтобы получить максимальный выигрыш.

Критерий Гурвица (критерий пессизма-оптимизма). В соответствии с этим критерием оптимальным считается действие , для которого достигается

,

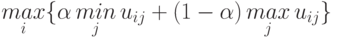где .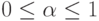

Из приведенного условия видно, что критерий Гурвица является взвешенной средней из наименьших и наибольших выигрышей для принятого коэффициента . В частности, при 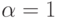критерий Гурвица соответствует критерию Вальда. Заметим, что минимальный критерий учитывает только наибольший выигрыш, получаемый в результате применения любой стратегии, и безразличен к любым другим вариантам.

Критерий Байеса (Лапласа). В соответствии с этим критерием оптимальным считается действие, которому соответствует

.

Следовательно, критерий Байеса (Лапласа) исходит из того, что раз совершенно неизвестно, какое из состояний имеет место, то нужно поступать так, как будто они равновероятны.