|
мне задали дистанционное задание на сертификат,но я не могу его найти |
Типы систем массового обслуживания и критерии эффективности
Механизмы оценки эффективности системы АТС на основе элементов теории массового обслуживания
Задачу обслуживания линий связи можно рассматривать как ситуацию, когда появляется необходимость в обслуживании требований (телефонных разговоров или сеансов доступа к сети Internet), поступающих в систему. Система телекоммуникаций обладает ограниченными возможностями для удовлетворения запросов клиентов, что приводит к образованию очереди. Основной задачей телекоммуникации является сокращение (в идеале — ликвидация) таких очередей при полной загрузке линий связи с целью их экономичного использования, ведь их техническая эксплуатация требует материальных вложений. Поэтому достаточно сложную задачу, имеющую множество ограничений, как со стороны уменьшения отказа в обслуживании, так и в полной загрузки линии, можно решать только комплексно.
Созданное программное обеспечение будет являться инструментом анализа такой задачи. Естественно, на основе результатов исследований, решение будет принимать специалист экономического подразделения организации, предоставляющей услуги телекоммуникаций.
Задача анализа линий связи на междугородней автоматической станции или линий связи с провайдером доступа к сети Internet относится к задачам теории массового обслуживания. Общей особенностью таких задач является случайный характер исследуемых явлений (сеансы связи), так как количество требований на обслуживание, временные интервалы между их поступлениями и длительность обслуживания случайны. Основные элементы исследуемой системы следующие: входящий поток требований, который лучше всего реализовать с использованием систем управления базами данных, линии связи (будем называть их приборами), очередь требований, которую можно представить в виде реестров предоставляемых услуг телекоммуникаций за отчетный период.
Данная система относится к системе с потерями, так как всякое вновь поступившее требование (выход на междугороднюю станцию по системе "Кварц" либо соединение с линией провайдера), застав все линии связи занятыми, покидает систему. В системах массового обслуживания с потерями используют математическую модель распределения Эрланга [2].
Математическая модель решения задачи анализа работы линий связи
Процесс поступления в систему массового обслуживания потока требований (выходов на междугороднюю станцию клиентов) является вероятностным. Он представляет собой поток однородных событий, поступающих через случайные промежутки времени.
Рассмотрим однородное событие  , следующее одно за другим через случайные промежутки времени. Число
, следующее одно за другим через случайные промежутки времени. Число  реализаций события
реализаций события  , происходящее в течение интервала времени
, происходящее в течение интервала времени  , является случайной величиной, которую обозначим через
, является случайной величиной, которую обозначим через 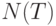 ; вероятность того, что
; вероятность того, что  , обозначим
, обозначим 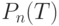 . [3]
. [3]
Определим распределение вероятностей для такого потока, (то есть найдем величины 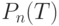 , где
, где 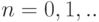 .). Для любого времени
.). Для любого времени  имеем
имеем
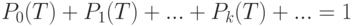
Вероятность того, что событие  произойдет более одного раза в интервале времени
произойдет более одного раза в интервале времени 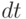 , есть величина бесконечно малая по сравнению с
, есть величина бесконечно малая по сравнению с 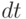 . Вероятность того, что событие
. Вероятность того, что событие  произойдет 1 раз, пропорциональна
произойдет 1 раз, пропорциональна 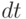 и равна
и равна  , следовательно
, следовательно 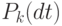 , где
, где 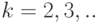 . бесконечно малые, поэтому
. бесконечно малые, поэтому 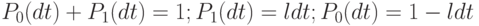 После аналитического преобразования Лапласа получим:
После аналитического преобразования Лапласа получим:
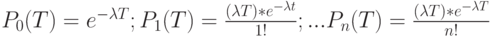
Таким образом, однородный поток заявок описывается распределением Пуассона.
В установившемся режиме Эрлангом были найдены следующие зависимости.
- Вероятность того, что обслуживанием заняты
 линий связи:
линий связи:
- Среднее число линий связи , занятых обслуживанием (коэффициент загрузки линий связи).
- Коэффициент простоя линий связи.
Эти зависимости выведены Эрлангом при условии, что время обслуживания распределено экспоненциально, они верны также и для произвольного абсолютно непрерывного закона распределения обслуживания [3,4], что позволяет распространить рамки применимости формул Эрланга на задачи анализа эффективности использования линий связи.
Для выбора алгоритма поиска оптимального числа линий связи были проанализированы критерии Лапласа, Гурвица, Сэвиджа и Вальда.
Метод Сэвиджа неприемлем для анализа, так как существует необходимость построения матриц "сожалений", а это значительно усложняет алгоритм обработки данных. Метод Лапласа является поиском усредненного значения, а значит, не является достаточно гибким при решении задачи проекта. Критерии Вальда и Сэвиджа ориентированы на пессимистическое и оптимистическое решение задачи соответственно, поэтому для того, чтобы программа нашла большее применение, этими методами также невозможно решать задачу для любых ситуаций принятия решений. Выбор останавливается на методе Гурвица, так как этот критерий позволяет задавать коэффициент доверия в различных ситуациях и поэтому является наиболее приемлемым для использования его в алгоритме нахождения оптимального решения задачи.
В задачах по принятию стратегии возникает множество трудностей с решением, так как мы имеем большое число критериев, которые не всегда согласованы между собой, а высокая степень неопределенности, обусловленная недостаточной информацией для обоснования принятия решения, существенно затрудняет поиск решения.
Одним из определяющих факторов в этой задаче являются состояния, в которых могут находится линии связи в зависимости от коэффициента простоя 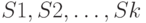 , — эти коэффициенты нам неизвестны.
, — эти коэффициенты нам неизвестны.
Тогда математическую модель в условиях неопределенности можно сформулировать следующим образом [2]:
имеется некоторая матрица  размерностью
размерностью  .
.
Элементы этой матрицы  можно рассматривать как полезность результата
можно рассматривать как полезность результата 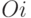 (которое складывается из среднего между коэффициентом простоя и вероятностью, что все линии связи свободны) при использовании стратегии
(которое складывается из среднего между коэффициентом простоя и вероятностью, что все линии связи свободны) при использовании стратегии 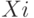 — выбора числа линий связи.
— выбора числа линий связи.
Критерий Гурвица основан на следующих двух предположениях: среда может находиться в самом невыгодном состоянии с вероятностью 1-a, т.е. с вероятностью, что поток заявок на обслуживание очень низкий, и в самом выгодном — с вероятностью  — коэффициент доверия.
— коэффициент доверия.
Тогда решающее правило Гурвица записывается так [5]:
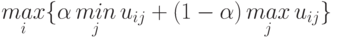
Таким образом, нетрудно составить алгоритм решения задачи поиска оптимального количества линий связи (так как все исходные данные получены на этапе анализа работы линий связи).
Хранение исходных данных организовано по средствам СУБД Access.
Первая версия программного обеспечения реализована на Visual Basic. Данное средство удачно подходит для решения задач оптимизации в проекте, так как имеет полную совместимость с Access и более удобные средства как для описания алгоритмов решаемых задач, так и для проектирования интерфейса создаваемого программного продукта.
Вторая версия программного обеспечения по анализу работы линий связи выполняется на C # в Visual Studio.NET.
В качестве основного языка объектно-ориентированной платформы выбран C #.
C # создан на базе опыта разработки других языков программирования:
- Высокая производительность (от C).
- Объектно-ориентированная структура (от С++).
- Сбор мусора, высокая безопасность (от Java).
- Быстрая разработка (от Visual Basic).
Поэтому C # — язык идеально подходящий для разработки компонентных  -уровневых распределенных веб-приложений Visual Studio.NET.
-уровневых распределенных веб-приложений Visual Studio.NET.
Таким образом, выбранный инструментарий для написания программы по анализу линий связи является оправданным как для решения самой задачи, так и исходя из современных требований к программному обеспечению.
В данной работе новыми являются:
- методы создания математического аппарата оценки параметров загруженности линий связи на междугородних телефонных станциях и линиях провайдеров;
- создание веб- и Windows- приложений на платформе .NET, работающих как на локальном компьютере, так и в Internet.
Задача 2.
Пусть через противолодочный рубеж прорываются подводные лодки. Известно, что в среднем за сутки через рубеж проходят три подводные лодки. Моменты начала форсирования неизвестны, но можно предполагать, что поток прорывающихся подводных лодок простейший. Необходимо определить, какое количество противолодочных самолетов  должно осуществлять патрулирование на рубеже для того, чтобы в момент появления очередной подводной лодки с вероятностью, не меньшей 0,9, хотя бы один самолет был свободен (осуществлял поиск). Предполагается, что после появления очередной подводной лодки самолет занят ее "обслуживанием". Среднее время занятости самолета
должно осуществлять патрулирование на рубеже для того, чтобы в момент появления очередной подводной лодки с вероятностью, не меньшей 0,9, хотя бы один самолет был свободен (осуществлял поиск). Предполагается, что после появления очередной подводной лодки самолет занят ее "обслуживанием". Среднее время занятости самолета ![M[\gamma]=2,4час](/sites/default/files/tex_cache/bf944f55dd3dfd8e93a74f4431a9f7dc.png) . Точное значение занятости самолета неизвестно, но можно предполагать, что оно случайно и подчинено показательному закону. В такой постановке задачу можно рассматривать как одну из задач массового обслуживания. В качестве критерия эффективности выбрана вероятность того, что хотя бы один из самолетов ПЛО был свободен к моменту появления лодки на рубеже. Предполагается, что вероятность обнаружения лодки на рубеже ПЛО равна единице.
. Точное значение занятости самолета неизвестно, но можно предполагать, что оно случайно и подчинено показательному закону. В такой постановке задачу можно рассматривать как одну из задач массового обслуживания. В качестве критерия эффективности выбрана вероятность того, что хотя бы один из самолетов ПЛО был свободен к моменту появления лодки на рубеже. Предполагается, что вероятность обнаружения лодки на рубеже ПЛО равна единице.
В абстрактной постановке эта задача формулируется следующим образом.
Имеется обслуживающая система, состоящая из  аппаратов. Она относится к числу систем с потерями, то есть требование, поступившее в момент, когда все обслуживающие аппараты заняты, покидает систему. Если в системе в момент поступления требования (лодки) есть хотя бы один свободный аппарат (самолет ПЛО), то он немедленно приступает к обслуживанию требования (лодки). Каждый аппарат (самолет) может одновременно обслужить только одно требование (лодку). Для рассматриваемой задачи безразлично, относится система к числу упорядоченных или нет. Время обслуживания одного требования одним аппаратом подчинено показательному закону с параметром
аппаратов. Она относится к числу систем с потерями, то есть требование, поступившее в момент, когда все обслуживающие аппараты заняты, покидает систему. Если в системе в момент поступления требования (лодки) есть хотя бы один свободный аппарат (самолет ПЛО), то он немедленно приступает к обслуживанию требования (лодки). Каждый аппарат (самолет) может одновременно обслужить только одно требование (лодку). Для рассматриваемой задачи безразлично, относится система к числу упорядоченных или нет. Время обслуживания одного требования одним аппаратом подчинено показательному закону с параметром  . Напомним, что это означает следующее: вероятность того, что время обслуживания
. Напомним, что это означает следующее: вероятность того, что время обслуживания  меньше
меньше  , равна
, равна

а 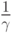 есть математическое ожидание времени обслуживания, равное 2,4 часа.
есть математическое ожидание времени обслуживания, равное 2,4 часа.
В систему на обслуживание поступает простейший поток требований (лодок) с параметром  . Вероятность поступления равно
. Вероятность поступления равно  требований за время
требований за время  равна
равна
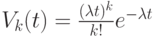 ,
,
где  — математическое ожидание числа требований за единицу времени.
— математическое ожидание числа требований за единицу времени.
Не останавливаясь на решении этой задачи, приведем некоторые показатели, характеризующие состояние системы.
Вероятность того, что в обслуживающей системе находится ровно  требований, то есть занято
требований, то есть занято  обслуживающих аппаратов, будет
обслуживающих аппаратов, будет
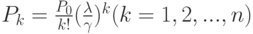 .
.
Вероятность того, что все обслуживающие аппараты свободны, будет
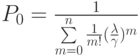
Здесь  — число обслуживающих аппаратов системы (число самолетов ПЛО).
— число обслуживающих аппаратов системы (число самолетов ПЛО).
Вероятность отказа очередному требованию в обслуживании будет
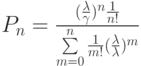 .
.
Среднее число занятых обслуживающих аппаратов:
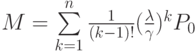
Для получения вероятности (  ) того, что хотя бы один из обслуживающих аппаратов (самолетов) будет свободен, можно воспользоваться величиной
) того, что хотя бы один из обслуживающих аппаратов (самолетов) будет свободен, можно воспользоваться величиной 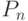 — вероятностью отказа очередному требованию в обслуживании, которая равна вероятности того, что все обслуживающие аппараты заняты.
— вероятностью отказа очередному требованию в обслуживании, которая равна вероятности того, что все обслуживающие аппараты заняты.
Искомая вероятность 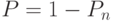 . В нашем примере
. В нашем примере 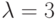 (среднее число прорывающихся подводных лодок в сутки):
(среднее число прорывающихся подводных лодок в сутки):
![\gamma =\frac{1}{M[\gamma]}=10](/sites/default/files/tex_cache/1a523c57ff538770a2ae0448cac79b3f.png) , так как
, так как ![M[\gamma]=2,4 час=0,1 суток](/sites/default/files/tex_cache/80d849a9f708e4b134add0bac7938268.png) .
.
Таким образом, нужно найти  из условия
из условия 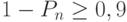 или
или  . При
. При 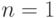 вероятность того, что все самолеты заняты "обслуживанием" подводных лодок,
вероятность того, что все самолеты заняты "обслуживанием" подводных лодок, 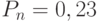 . Следовательно, одного самолета мало для обеспечения заданной надежности обслуживания.
. Следовательно, одного самолета мало для обеспечения заданной надежности обслуживания.
Таким образом, из двух самолетов, находящихся на рубеже, с вероятностью 0,97 хотя бы один из них будет свободен в любой момент времени.
Интересно, насколько при этом будут заняты "работой" самолеты. Количественно эту занятость можно описать величиной  — средним числом занятых самолетов. При
— средним числом занятых самолетов. При  эта величина равна
эта величина равна 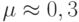 , то есть в среднем 85% времени каждый самолет будет свободен.
, то есть в среднем 85% времени каждый самолет будет свободен.

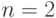
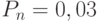 , поэтому
, поэтому 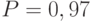 .
.