Теория игр

Введение

Лекции "Теория игр" , "Метод вычисления оптимальных стратегий" , "Вычисление оптимальных стратегий в бесконечных играх" посвящены обоснованию решений в условиях неполной информации о фактической обстановке, когда складываются так называемые конфликтные ситуации, исход которых зависит от действий двух сторон с противоположными интересами. Излагается сущность теории игр и раскрывается область ее применения; формулируются правила построения теоретико-игровых моделей; дается классификация таких моделей, и описываются математические методы, с помощью которых находятся оптимальные способы действий.

Основные понятия теории игр

В ситуациях, называемых конфликтными, предугадать исход и тем более определить действия, при которых этот исход оказался бы наиболее благоприятным, оказывается чрезвычайно сложно. Предположим, что сторона обладает способами действий 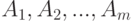, на каждой из которых сторона может ответить одним из способов 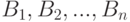. Пусть результат взаимных действий характеризуется критерием эффективности , который представляет собой выигрыш стороны . Тогда конфликтную ситуацию можно представить в виде матрицы эффективности (рис. 8.a.).

Рис. 8.a.

Из рисунка 8.a. видно, что если сторона выбирает способ , то исход конфликта, характеризуемый критерием эффективности 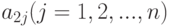, будет целиком зависеть от выбора способа действий стороной . Аналогичный вывод можно сделать в отношении любого другого способа действий стороны . В этих условиях естественным подходом к выбору оптимального способа является сравнение между собой всех способов действия стороны при условии выбора стороной каждого из способов.

Например, сравнивая способ со способом , можно в частном случае установить, что способ обеспечивает достижение лучшего результата, если каждый элемент его строки больше соответствующего элемента (по столбцам) строки способа . Если путем подобного сравнения найдется такой способ 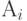, каждый элемент строки которого больше соответствующего элемента (по столбцам) любой другой строки, то целесообразно применить способ 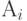. В остальных случаях выбор способа стороной может быть осуществлен только для определенной гипотезы о действиях стороны .

Другой естественный подход состоит в определении математического ожидания величины критерия эффективности для -го способа действия стороны по формуле

,

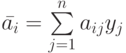где 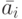— математическое ожидание величины критерия эффективности при выборе способа действия ;

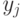— вероятность выбора стороной способа действия .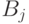

Тогда способы действия стороны можно сравнить по величине 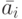и выбрать тот, при котором 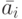будет максимальным. При этом как в первом, так и во втором случае для обоснования решения достаточно использовать методы оптимизации.

Таким образом, для применения в условиях конфликтной ситуации обычных методов оптимизации необходимо задаться или гипотезой о действиях противника, или законом распределения их вероятностей. Однако для конфликтных ситуаций как раз характерным является то, что отдать предпочтение какой-либо гипотезе не представляется возможным, а методов определения законов распределения вероятности выбора противником своих способов действий просто не существует.

В связи с этим возникает необходимость в теории специфического класса математических моделей принятия оптимальных решений. Такой теорией является теория игр .

Теорию игр можно рассматривать, с одной стороны, как раздел исследований операций, а с другой — как его уровень. В качестве раздела исследования операций теория игр представляет теорию математических моделей принятия оптимальных решений в конфликтных ситуациях. Как уровень исследования операций теория игр является теорией математических моделей принятия решений в условиях неопределенности. Однако не следует полагать, будто теория игр занимается вопросами принятия решений при полном неведении об обстановке. Известные элементы обстановки определяют множество способов действий сторон и значения критерия эффективности как функции, заданной на этом множестве. Неизвестные элементы обуславливают отсутствие любой, даже вероятностной информации о возможных реализациях того или иного способа действий противника. Таким образом, любую неопределенность можно расчленить на известную и неизвестную части, построить теоретико-игровую модель, на основании которой определяется оптимальное решение.

Для применения теории игр нужна существенная схематизация конфликтной ситуации и представление ее в виде игры, в которой противники, именуемые игроками, имеют противоположные цели и располагают различными путями для их достижения. Причем обязательным является то, что достижение одним игрокам своей цели находится в непосредственной зависимости от выбора способа действий другим игроком. Более того, отличительная особенность игры по сравнению с реальной конфликтной ситуацией состоит в том, что первая ведется по заранее определенным правилам. В этом и заключается основное ограничение в применении теории игр. Ведь если теоретико-игровой подход, безусловно, правомерен в любой игре, то не всегда можно построить соответствующую математическую модель для конкретных условий обстановки.

Основное значение теории игр состоит в том, что она дает ориентацию тогда, когда применение другого математического аппарата невозможно из-за отсутствия необходимой информации о действиях противника, а времени и, самое главное, других эффективных способов нет.

Применение теории игр для обоснования оптимального решения требует представления конфликтной ситуации в виде некоторой игры, которая по своему содержанию и форме является ее математической моделью.

Для построения модели конфликтной ситуации прежде всего должны быть сформулированы правила игры, то есть система условий, которая определяет возможные варианты действий игроков, последовательность ходов, объем информации каждого игрока о поведении другого и о функции выигрыша .

Возможные варианты способов действий вытекают непосредственно из анализа конфликтной ситуации.

Выбор одного из возможных вариантов в процессе игры называется ходом .

Заранее определенная последовательность ходов в зависимости от информации о ходах противника и о случайно изменяющихся параметрах, законы распределения которых считаются заданными, называется стратегией игрока . Каждая стратегия предопределяет поведение игрока во все моменты игры, когда он должен делать выбор одного из всевозможных способов действий. Она может быть очень плохой или очень хорошей, но для анализа игры существенно описать все возможные планы или стратегии каждого игрока.

Совокупность сделанных игроками ходов в соответствии с выбранными ими стратегиями определяет ситуацию игры, которая является моделью складывающейся обстановки в результате конкретных действий, предпринятых противоположными сторонами. Ситуация, на основании которой определяется исход игры, называется заключительной .

Каждой заключительной ситуации всегда соответствует определенное значение критерия эффективности. Правило, по которому каждой заключительной ситуации ставится в соответствии величина критерия эффективности, называется функцией выигрыша . Это название обусловлено тем, что каждое ее значение можно представить как выигрыш, получаемый игроком в зависимости от сделанных ходов. На величину выигрыша оказывают влияние не только действия игроков, но и факторы, которые не находятся под их управлением. К таким факторам относятся эффективность, или стоимость имеющихся в распоряжении игроков сил и средств, их количество, гидролого-метеорологические условия и так далее. Поэтому при описании функции выигрыша учитываются не только возможные способы действий игроков, но и факторы, независимые от игроков. Однако по своей сущности функция выигрыша представляет выигрыш каждого игрока только как функцию стратегий, применяемых игроками. В этом смысле выигрыш является связующим звеном между множеством стратегий одного игрока и множеством стратегий другого; функция же выигрыша указывает, сколько один игрок может выиграть у другого, если первый выбирает конкретную какую-либо стратегию из множества стратегий, а другой игрок выбирает какую-либо стратегию из своего множества.

Таким образом, выигрыш – это оценка ожидаемых результатов всех возможных сочетаний стратегий одного игрока со стратегиями другого. Для получения таких оценок могут применяться методы теории вероятностей, теории массового обслуживания, теории управления запасами, теории поиска и различные экономические показатели. Следовательно, теория игр исходит из заранее определенных значений того или иного критерия эффективности для конкретного сочетания стратегий обоих игроков, то есть принимается, что функция выигрыша задана.

Теоретико-игровые модели боевых действий классифицируются в зависимости от числа последовательных ходов и возможных способов действий игроков, характера и объема информации, доступной каждому игроку относительно действий другого, а также отношения каждого из игроков к значению функции выигрыша.

В зависимости от числа возможных способов действий игры подразделяются на конечные и бесконечные. Конечной называется игра, в которой у каждого игрока имеется конечное число возможных способов действий. В бесконечной игре по крайней мере один из игроков имеет бесконечное множество возможных способов действий.

Число последовательных ходов у любого из игроков определяет подразделение игр на одноходовые и многоходовые, или позиционные. В одноходовой игре каждый игрок делает только один выбор из возможных вариантов и после этого устанавливает исход игры.

Многоходовая, или позиционная, игра развивается во времени, представляя собой ряд последовательных этапов, каждый из которых наступает после хода одного из игроков и соответствующего изменения обстановки.

Многоходовые игры в зависимости от характера и объема информации каждого игрока о сделанных ходах противником подразделяются на два класса: игры с полной информацией и игры с неполной информацией. В играх с полной информацией каждый игрок на каждом этапе знает результаты всех предыдущих ходов. В зависимости от отношения каждого из игроков к значению функции выигрыша игры подразделяются на антагонистические и неантагонистические. В антагонистических играх интересы ее участников прямо противоположны. Это означает, что сколько один игрок выиграл, то столько же другой проиграл. В этих условиях каждый игрок стремится обеспечить себе максимальный выигрыш, а противнику максимальный проигрыш. Это приводит к тому, что выигрыш одного игрока соответствует проигрышу другого, Поэтому можно считать, что суммарный выигрыш обоих игроков антагонистической игры во всех ситуациях равен нулю. Отсюда эти игры иногда называют играми с нулевой суммой или нулевыми играми.

В неантагонистических играх игроки преследуют разные, но не прямо противоположные цели. Отсутствие антагонизма в смысле "равенства значений функций выигрыша по величине и противоположности по знаку" приводит к одному из классов неантагонистических игр, называемому биматричными играми .

Одноходовая конечная антагонистическая игра является теоретико-игровой моделью конфликтной ситуации, в которой противники для достижения диаметрально противоположных целей делают по одному выбору (ходу) из конечного числа возможных способов действий. В соответствии с выбранными способами действий (стратегиями) определяется достигаемый результат. Функция выигрыша в такой игре задается матрицей. (табл. 8.b).

Рис. 8.b.

В этой матрице строки всегда для стратегий выигрывающего (максимизирующего) игрока, то есть игрока, который стремится к максимизации критерия эффективности (игрок I).

Столбцы отводятся для стратегий проигрывающего игрока, то есть игрока, который стремится к минимизации критерия эффективности (игрок II). Клетки матрицы, стоящие на пересечении строк и столбцов, представляют результаты заключительных ситуаций и заполняются числами — значениями критерия эффективности, характеризующего выигрыш игрока I и соответственно проигрыш игрока II.

Обычно матрицу, имеющую строк и столбцов, называют 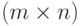матрицей и обозначают 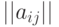. Соответственно игру называют ( 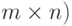игрой.

Позиционная (многоходовая) игра является теоретико-игровой моделью конфликтной ситуации, в которой противники для достижения своих целей последовательно делают по одному выбору (ходу) из конечного числа возможных способов действий на каждом этапе развития этой ситуации.

Процесс сведения позиционной игры к игре, описываемой матрицей, называется нормализацией , а получающаяся игра – игрой в нормальной форме . Действительно, в этой игре значения функции выигрыша можно всегда записать в виде прямоугольной таблицы (матрицы), строки которой соответствуют стратегиям игрока I, а столбцы – стратегиям игрока II.