Дискретное программирование

Предмет дискретного программирования

Настоящая лекция посвящена дискретным задачам математического программирования. Наиболее изученными задачами этого класса являются целочисленные задачи линейного программирования, то есть задачи линейного программирования, в которых на все переменные (либо на их часть) наложено дополнительное требование целочисленности. В первом из этих случаев обычно говорят о полностью целочисленных, а во втором – о частично целочисленных задачах. Разумеется, аналогичным образом можно определить целочисленные (частично целочисленные) варианты и для более общих задач оптимального программирования – можно говорить, например, о задачах выпуклого целочисленного программирования и тому подобное.

От целочисленных задач принято отличать так называемые дискретные задачи математического программирования, в которых областью допустимого изменения каждой переменной является не множество целых неотрицательных чисел, а некоторое заданное конечное множество. Такие задачи (на конечных множествах) могут быть формально сведены к целочисленным.

Исследования в этом направлении, начатые еще в шестидесятые годы прошлого столетия, к настоящему времени продвинулись настолько далеко, что сейчас мы уже вправе говорить о самостоятельном разделе математического программирования – дискретном программировании. В литературе употребляется также термин " целочисленное программирование " и реже – " комбинаторное программирование ". Однако нам представляется, что термин " дискретное программирование " наиболее полно отражает специфику вопроса, хотя при его использовании и возникает некоторая опасность смешения дискретного программирования и, скажем, дискретного анализа.

Постановка задачи линейного программирования

Линейное программирование является составной частью более общего метода — математического программирования. Математическое программирование позволяет находить наилучшие планы распределения ограниченных ресурсов для достижения требуемой цели – решения задачи. Линейное программирование может быть использовано как один из методов оптимизации решения. Наилучший результат здесь достигается не за счет выделения дополнительных сил и средств или иных ресурсов, а за счет их рационального распределения.

Решение, наилучшим образом соответствующее целевой установке и удовлетворяющее условиям задачи, называется оптимальным планом .

Линейное программирование от других видов математического программирования отличается тем, что математическая модель, соответствующая целевой установке задачи, может быть записана с помощью линейных соотношений вида:

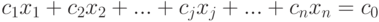( 6.1)

где 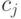— - — известные коэффициенты;

- - — неизвестные переменные .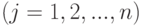

В общем виде постановка задачи линейного программирования выглядит следующим образом.

Условия задачи задаются в виде системы линейных уравнений или неравенств, которые представляют ограничения, налагаемые на использование имеющихся ресурсов:

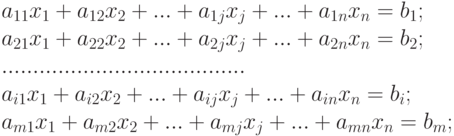( 6.2)

где

.

Искомые величины 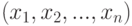не могут быть отрицательными; — известные постоянные величины, характеризующие условия задачи.

Целевая функция задается в виде такой линейной формы:

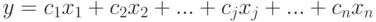( 6.3)

где 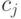— постоянные коэффициенты, которые обычно называют коэффициентами стоимости .

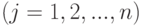Целевую функцию по условиям задачи требуется обратить в минимум или максимум. В некоторых задачах выражения (6.2.) задаются в виде неравенств. В этих случаях, вводя в каждое линейное ограничение дополнительные неотрицательные неизвестные

,

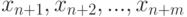можно привести систему линейных ограничений к виду (6.2.).

Геометрическая интерпретация задачи линейного программирования

Геометрическую интерпретацию задачи линейного программирования рассмотрим на примере.

Пример

Четыре вида овощей 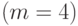необходимо распределить по шести транспортным средствам .

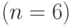Распределение овощей по транспортным средствам сопряжено с необходимостью учета ряда ограничений, которые могут быть описаны системой четырех уравнений с шестью неизвестными, аналогичными системе 6.2.

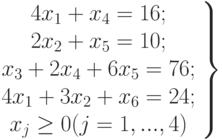( 6.4)

Смысл первого уравнения в нашем примере означает, что овощ типа 1, общий ресурс которого составляет 16 единиц, может размещаться в количестве четырех единиц на транспортном средстве первого типа и одной единицы на транспортном средстве четвертого типа. Аналогично и второе уравнение и так далее.

Последнее условие говорит о том, что число типов транспортного средства не может быть отрицательным.

Необходимо определить, какое количество транспортного средства каждого типа следует иметь, чтобы общие потери в них были минимальными.

Оплата за конкретное транспортное средство (в тысячах рублей) задана следующей таблицей.

Тип единицы транспорта,	1	2	3	4	5	6
Стоимость перевозки на транспорте данного типа,	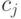0,4	0,5	0,2	0,8	0,6	0,3

В соответствии с приведенными данными, целевая функция, подлежащая оптимизации, примет вид:

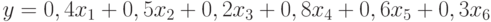( 6.5)

Решение задачи сводится к выполнению ограничений, заданных уравнением (6.4.)

В этом примере, когда 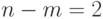, каждое из ограничительных линейных уравнений (6.4.), а также линейная функция (6.5.), могут быть представлены геометрически в двухмерном пространстве (на плоскости), что дает возможность весьма наглядно интерпретировать основные идеи метода линейного программирования.

Геометрическая интерпретация задачи линейного программирования. Чтобы иметь возможность наглядно представить ограничения и целевую функцию на графике, необходимо выразить все неизвестные через две независимые величины, например, и , соответствующие координатным осям, относительно которых будет производиться построение (рис. 6.1). Из уравнения (6.4.) следует:

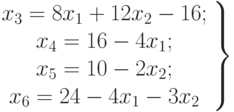( 6.6)

А целевая функция примет такой вид:

.

Из сопоставления уравнений (6.6.) и последнего из ограничений (6.2.) следует:

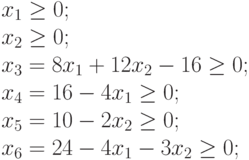( 6.8)

Каждому из неравенств (6.8.) на графике рис. 6.1 соответствует полуплоскость, в пределах которой находятся все допускаемые данным неравенством значения переменной величины .

Так, например, неравенству 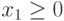соответствует полуплоскость вправо от оси (граница ее заштрихована).

Неравенству

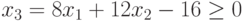
соответствует полуплоскость вправо и вверх от линии, соответствующей значению данного неравенства (при ).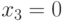

Уравнение этой линии

.

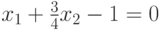Таким же образом можно построить границы, определяемые другими уравнениями.

Неравенствам (6.8.) соответствует некоторая область – шестиугольник , образованный границами упомянутых выше полуплоскостей. Эта область может быть названа областью допустимых планов, поскольку любая точка в ее пределах отвечает требованиям наложенных ограничений (6.4.).

Из всех доступных планов нас интересует оптимальный план, при котором функция цели достигает минимума.

Целевой функции соответствует семейство параллельных прямых. Рассмотрим одну из них, проходящую через начало координат, что будет иметь место при .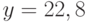

При этом

.

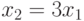Интересующая нас прямая 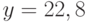, как видно из рисунка 6.1, имеет наклон вправо от оси . Задаваясь различными значениями , получим семейство прямых линий, параллельных прямой 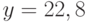, которая проходит через точку 0. При этом чем меньше будет , тем, очевидно, правее располагается соответствующая прямая.

Поскольку мы добиваемся минимального значения , нас будет интересовать прямая, расположенная в наибольшем удалении вправо от прямой 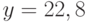и проходящая через многоугольник , — прямая .

Как видно из рисунка 6.1, единственной точкой, соответствующей оптимальному плану, будет та вершина многоугольника , которая одновременно принадлежит области допустимых планов и отвечает требованию минимизации целевой функции — вершина .

Итак минимум целевой функции достигается в вершине многогранника. Существует теорема о том, что для любой задачи линейного программирования найдется вершина многогранника допустимых решений, в которой целевая функция достигает своего минимального (максимального) значения.

Рис. 6.1.