|
мне задали дистанционное задание на сертификат,но я не могу его найти |
Базовые идеи и методы теории вероятностей
Определения
Среднеквадратичным значением случайной величины  называется математическое ожидание
называется математическое ожидание 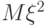 :
:
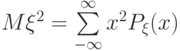
для дискретных величин,
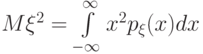
для непрерывно распределенных величин. Имеет место следующее неравенство Чебышева: каково бы ни было 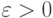 ,
,
 |
( 3.1) |
Неравенство Чебышева показывает, что если среднеквадратичное значение 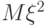 мало по сравнению с
мало по сравнению с 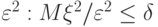 и практически можно пренебречь возможностью осуществления события
и практически можно пренебречь возможностью осуществления события  малой вероятности
малой вероятности 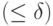 , то будет малой и сама случайная величина
, то будет малой и сама случайная величина 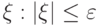 . В частности, если
. В частности, если 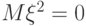 , то с вероятностью 1 и
, то с вероятностью 1 и  .
.
Дисперсией случайной величины  , обозначаемой
, обозначаемой 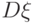 , называется среднеквадратичное значение
, называется среднеквадратичное значение 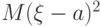 разности
разности  , где
, где 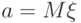 — математическое ожидание случайной величины
— математическое ожидание случайной величины  . Имеет место следующая формула:
. Имеет место следующая формула:
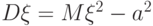 |
( 3.2) |
В самом деле,
 .
.
Очевидно,
 |
( 3.3) |
и для любой постоянной 
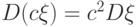 |
( 3.4) |
Пусть 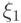 и
и 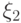 — независимые случайные величины. Тогда дисперсия их суммы может быть найдена по формуле
— независимые случайные величины. Тогда дисперсия их суммы может быть найдена по формуле
 |
( 3.5) |
Пусть 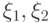 — случайные величины,
— случайные величины, 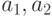 — их математическое ожидание, а
— их математическое ожидание, а  и
и 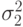 — их дисперсии, тогда
— их дисперсии, тогда
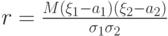 |
( 3.6) |
называется коэффициентом корреляции этих 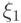 ,
, 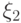 случайных величин.
случайных величин.
Коэффициент корреляции является простейшей характеристикой связи случайных величин. Если случайные величины независимы, то их коэффициент корреляции равен нулю. Коэффициент корреляции всегда лежит в пределах

причем, если  или
или 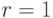 , то случайная величина
, то случайная величина 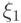 есть просто линейная комбинация вида
есть просто линейная комбинация вида
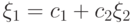 ,
,
где 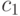 ,
, 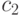 — некоторые постоянные.
— некоторые постоянные.
Закон больших чисел
Рассмотрим независимые случайные величины 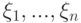 имеющие одинаковое распределение вероятностей (и, в частности, одинаковые математические ожидания
имеющие одинаковое распределение вероятностей (и, в частности, одинаковые математические ожидания 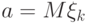 и дисперсии
и дисперсии 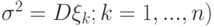 . Рассмотрим среднее арифметическое значение этих величин
. Рассмотрим среднее арифметическое значение этих величин

Имеем
 .
.
Используя неравенство Чебышева, получим
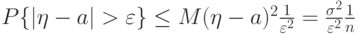 .
.
Очевидно, что, каково бы ни было 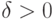 ? при достаточно большом
? при достаточно большом 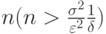 среднее арифметическое
среднее арифметическое 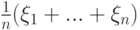 величин
величин 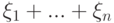 с вероятностью, не меньшей
с вероятностью, не меньшей 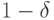 , будет содержаться в пределах
, будет содержаться в пределах
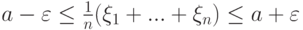 |
( 3.7) |
где 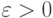 может быть заранее выбрано сколь угодно малым.
может быть заранее выбрано сколь угодно малым.
Этот факт носит название закона больших чисел. Если  и
и 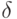 столь малы, что можно практически пренебречь возможностью наступления события вероятности
столь малы, что можно практически пренебречь возможностью наступления события вероятности 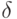 и различием величин, отличающихся друг от друга не более чем на
и различием величин, отличающихся друг от друга не более чем на  , то практически можно считать, что, несмотря на случайность, среднее арифметическое
, то практически можно считать, что, несмотря на случайность, среднее арифметическое 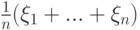 практически совпадает с математическим ожиданием (средним значением)
практически совпадает с математическим ожиданием (средним значением) 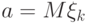 .
.
Распределение
Одинаковые, не зависимые между собой испытания, в каждом из которых рассматривается некоторое событие  , наступающее с положительной вероятностью
, наступающее с положительной вероятностью 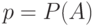 , называются испытаниями Бернулли. Само событие
, называются испытаниями Бернулли. Само событие  условно называется "успехом", а дополнительное событие
условно называется "успехом", а дополнительное событие 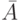 , наступающее в каждом из рассматриваемых испытаний с вероятностью
, наступающее в каждом из рассматриваемых испытаний с вероятностью 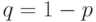 , условно называют "неудачей".
, условно называют "неудачей".
Если рассматривается  испытаний, то каждый элементарный исход
испытаний, то каждый элементарный исход  может быть описан, например, последовательностью длины n из 1 и 0 вида 10110001…, где стоящая на i-м месте 1 означает "успех" при i-м испытании, а 0 означает "неудачу". Вероятность
может быть описан, например, последовательностью длины n из 1 и 0 вида 10110001…, где стоящая на i-м месте 1 означает "успех" при i-м испытании, а 0 означает "неудачу". Вероятность 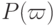 элементарного исхода
элементарного исхода 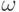 , при котором ровно
, при котором ровно  раз наступает "успех" и
раз наступает "успех" и 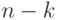 раз наступает "неудача", в силу независимости отдельных испытаний есть
раз наступает "неудача", в силу независимости отдельных испытаний есть
 .
.
Видно, что элементарные исходы 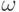 не являются равновероятными, когда
не являются равновероятными, когда  .
.
Рассмотрим случайную величину  , равную общему числу "успехов" в испытаниях Бернулли:
, равную общему числу "успехов" в испытаниях Бернулли:  , если при элементарном исходе
, если при элементарном исходе 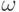 равно
равно  раз наступает "успех". Различных исходов
раз наступает "успех". Различных исходов 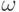 , приводящих к одному и тому же числу
, приводящих к одному и тому же числу  "успехов", столько же, сколько можно образовать различных комбинаций из
"успехов", столько же, сколько можно образовать различных комбинаций из  единиц и
единиц и 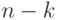 нулей. Число таких комбинаций равно числу сочетаний из
нулей. Число таких комбинаций равно числу сочетаний из  по
по  , что составляет
, что составляет  . Все эти исходы
. Все эти исходы 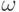 имеют одну и ту же вероятность
имеют одну и ту же вероятность  . Таким образом, распределение вероятностей случайной величины
. Таким образом, распределение вероятностей случайной величины  задается формулой
задается формулой
 |
( 3.8) |
Это – так называемое биномиальное распределение. Оно задается двумя параметрами: вероятностью отдельного "успеха"p и числом испытаний  . Случайная величина
. Случайная величина  есть сумма
есть сумма  независимых величин
независимых величин 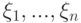 определяемых следующим образом:
определяемых следующим образом: 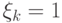 , если в
, если в  -м испытании наступает "успех", и
-м испытании наступает "успех", и  , если наступает "неудача":
, если наступает "неудача": 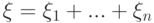 .
.
Имеем
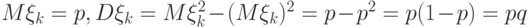 ,
,
откуда для математического ожидания и дисперсии случайной величины  получаем следующие выражения:
получаем следующие выражения:
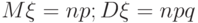 |
( 3.9) |
При большом числе испытаний  и сравнительно малой вероятности
и сравнительно малой вероятности  , когда каждый из "успехов" является сравнительно редким событием, но среднее число "успехов"
, когда каждый из "успехов" является сравнительно редким событием, но среднее число "успехов" 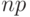 довольно значительно, приблизительно можно считать, что
довольно значительно, приблизительно можно считать, что
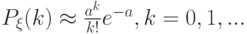 |
( 3.10) |
где  есть среднее число "успехов", а
есть среднее число "успехов", а 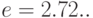 . — основание натуральных логарифмов.
. — основание натуральных логарифмов.
Говорят, что случайная величина  (принимающая лишь целочисленные значения 0, 1, …) имеет пуассоновское распределение вероятностей (распределена по закону Пуассона), если
(принимающая лишь целочисленные значения 0, 1, …) имеет пуассоновское распределение вероятностей (распределена по закону Пуассона), если
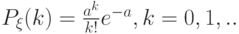 |
( 3.11) |
Это распределение задается одним-единственным неотрицательным параметром  , совпадающим со средним значением
, совпадающим со средним значением  :
:
 |
( 3.12) |
Действительно, воспользовавшись разложением  , справедливым при всех
, справедливым при всех  , имеем
, имеем 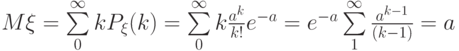 .
.
Приближенная формула 3.10. показывает, что при больших  и малых
и малых  случайная величина
случайная величина  , равна числу "успехов" в
, равна числу "успехов" в  испытаниях Бернулли (с вероятностью успеха
испытаниях Бернулли (с вероятностью успеха  ), приблизительно распределена по закону Пуассона с параметром
), приблизительно распределена по закону Пуассона с параметром  .
.
Было отмечено, что случайная величина  , равная числу "успехов" в
, равная числу "успехов" в  испытаниях Бернулли, совпадает с суммой
испытаниях Бернулли, совпадает с суммой  независимых величин
независимых величин 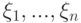 . Введем новое обозначение, положив
. Введем новое обозначение, положив
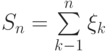 .
.
Пусть
 |
( 3.13) |
где 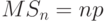 и
и  . Имеет место следующее предельное соотношение, называемое предельной теоремой Муавра-Лапласа
. Имеет место следующее предельное соотношение, называемое предельной теоремой Муавра-Лапласа
 .
.
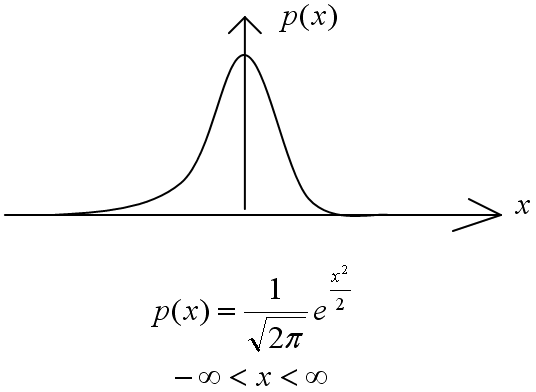
Фигурирующее здесь непрерывное распределение вероятностей с плотностью
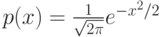
называется нормальным, или гауссовским, распределением. Как функция от  , плотность этого распределения вероятностей имеет график весьма специфической колоколообразной формы. Имеются таблицы функций нормального распределения –так называемой функции Лапласа.
, плотность этого распределения вероятностей имеет график весьма специфической колоколообразной формы. Имеются таблицы функций нормального распределения –так называемой функции Лапласа.
На практике очень многие случайные величины распределены нормально или почти нормально. Например, ошибки всевозможных измерений, представляющие собой сумму многих "элементарных", практически независимых, ошибок, вызванных отдельными причинами. По тому же закону распределяются, как правило, ошибки стрельбы, наведения, совмещения. Отклонения напряжения в сети от номинала также вызваны суммарным действием многих независимых причин, результаты действия которых складываются. Нормальному (или близкому) закону подчиняются такие случайные величины, как суммарная выплата страхового общества за большой период и тому подобное.