НОУ ИНТУИТ | Структуры и алгоритмы компьютерной обработки данных. Лекция 48: Задания

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

|

Вам нравится? Нравится 47 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Ключевые слова: параметр, Численным методом решения уравнений, метод итерации, метод Ньютона, Метод половинного деления, Абсолютной погрешностью, отрезок, алфавит, суффикс, индекс массива, симметрия, действительное число, матрица обратная, латинский квадрат, цена товара, строка данных, двумерный массив, бинарное дерево, сбалансированное дерево, критерии поиска, высота дерева, алгоритм, закономерность, значение, рекурсивная функция, натуральное число, счисление, прямой, координаты, cover, файл, переменная, целое число, анализ, время выполнения, определение, БНФ, список, looping, 1-грамматика, перевод строки, no-op, вывод, многочлен, коэффициенты, конкатенация, длина, быстрая сортировка, quicksort, путь, пробел, Произведение, сервер, полное имя файла, MS-DOS, полное имя, грани, вероятность, die, вещественное число, матрица, расстояние, плоскость, Абсолютной величиной, компьютер, равенство, программа, целый, множитель, форма Бэкуса-Наура, p-si, место, сегменты, высота, площадь, поле, архитектор, дерево, игра, система координат, диаметр, выражение, константы, бинарный оператор, деление, операторы, ячейка, выход, длина пути, ASCII, SMS, слово

Задание 1. Указатели

Решите уравнение указанным в варианте методом. Функцию передать как параметр с помощью указателя.

Численные методы решения уравнений

Довольно часто на практике приходится решать уравнения вида:

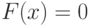( 2)

где функция F(x)

определена и непрерывна на некотором конечном или бесконечном интервале

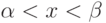
$\alpha < x < \beta$

Всякое значение $\overline{x}$ такое, что $F(\overline{x})\equiv 0$ , называется корнем уравнения, а нахождение этого значения и есть решение уравнения.

На практике в большинстве случаев найти точное решение возникшей математической задачи не удается. Поэтому важное значение приобрели численные методы, позволяющие найти приближенное значение корня. Под численными методами подразумеваются методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над числами, т.е. к тем действиям, которые выполняет компьютер.

Существует множество численных методов решения уравнений вида (1). Рассмотрим только три из них:

метод итераций;
метод Ньютона;
метод половинного деления.

Метод итераций

Представим уравнение 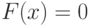F(x)=0 в виде:

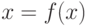( 2)

Это уравнение получается выделением из уравнения F(x) и переносом того, что осталось, т.е. f(x) , в левую часть уравнения. Иначе можно получить уравнение (2) следующим способом: левую и правую часть уравнения (1) умножить на произвольную константу $\lambda$ и прибавить к левой и правой части , т.е. получаем уравнение вида:

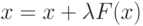$x=x+\lambda F(x)$

( 3)

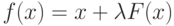где $f(x)=x+\lambda F(x)$ .

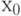На заданном отрезке [a; b] выберем точку х_0 – нулевое приближение – и найдем

потом найдем:

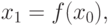
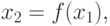
Таким образом, процесс нахождения корня уравнения сводится к последовательному вычислению чисел:

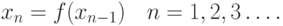
$x_n=f(x_{n-1})\quad n=1,2,3 \ldots .$

Этот процесс называется методом итераций.

Если на отрезке [a; b] выполнено условие:

$|f'(x_0)|\leq q<1,$

то процесс итераций сходится, т.е.

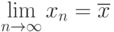
$\lim_{n\rightarrow\infty}x_n=\overline{x}$

Процесс итераций продолжается до тех пор, пока

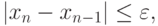
$|x_n-x_{n-1}|\leq\varepsilon,$

где – $\varepsilon$ заданная абсолютная погрешность корня

. При этом будет выполняться:

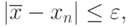
$|\overline{x}-x_n|\leq\varepsilon,$

Метод Ньютона

Пусть уравнение 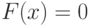F(x)=0 имеет один корень на отрезке [a; b] , причем F'(x) и F''(x) определены, непрерывны и сохраняют постоянные знаки на отрезке [a; b] .

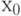Выберем на отрезке [a; b] произвольную точку х_0 – нулевое приближение. Затем найдем:

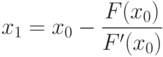
$x_1=x_0-\frac{F(x_0)}{F'(x_0)}$

потом

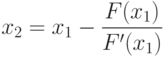
$x_2=x_1-\frac{F(x_1)}{F'(x_1)}$

Таким образом, процесс нахождения корня уравнения сводится к вычислению чисел 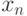x_n по формуле:

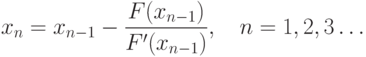
$x_n=x_{n-1}-\frac{F(x_{n-1})}{F'(x_{n-1})},\quad n=1,2,3\ldots$

Этот процесс называется методом Ньютона.

Процесс вычисления продолжается до тех пор, пока не будет выполнено условие:

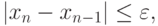
$|x_n-x_{n-1}|\leq\varepsilon,$

где – $\varepsilon$ заданная абсолютная погрешность корня

.

Точку 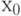х_0 необходимо выбирать так, чтобы выполнялось условие:

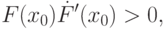
$F(x_0)\dot F'(x_0)>0,$

иначе метод не будет сходиться.

Метод половинного деления

Пусть уравнение 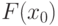F(x_0) имеет один корень на отрезке [a, b] . Функция непрерывна на отрезке [a, b] .

Метод половинного деления заключается в следующем:

Сначала выбираем начальное приближение, деля отрезок пополам, т.е.

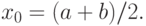
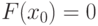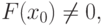Если F(x_0)=0 , то x_0 является корнем уравнения. Если $F(x_0)\neq 0,$ то выбираем тот из отрезков, на концах которого функция имеет противоположные знаки. Полученный отрезок снова делим пополам и выполняем действия сначала и т.д.

Процесс деления отрезка продолжаем до тех пор, пока длина отрезка, на концах которого функция имеет противоположные знаки, не будет меньше заданной точности $\varepsilon$ , т.е. пока не будет выполняться условие:

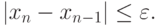
$|x_n-x_{n-1}|\leq\varepsilon.$

Варианты задания

№	Уравнение	Отрезок, содержащий корень	Метод	Значение корня с точностью 10^-4
1	$3\sin\sqrt{x}+0,35x-3,8=0$	[2;3]	Итераций	2,2985
2		[0;2]	Ньютона	1,0001
3	$x-\frac{1}{3+\sin 3,6x}=0$	[0;0,85]	Итераций	0,2624
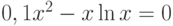
4	$0,1x^2-x\ln x=0$	[1;2]	Ньютона	1,1183
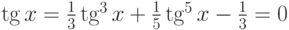
5	$\tg x=\frac13\tg^3 x+\frac15\tg^5 x-\frac13=0$	[0;8]	Половинного деления	0,3333
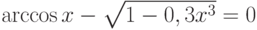
6	$\arccos x-\sqrt{1-0,3 x^3}=0$	[0;1]	Итераций	0,5629
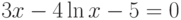
7	$3x-4\ln x-5=0$	[2;4]	Ньютона	3,2300
8	$\cos\frac{2}{x}-2\sin\frac{1}{x}+\frac{1}{x}=0$	[1;2]	Половинного деления	1,8756
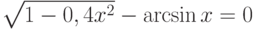
9	$\sqrt{1-0,4x^2}-\arcsin x=0$	[0;1]	Итераций	0,7672
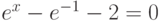
10	$e^x-e^{-1}-2=0$	[0;1]	Ньютона	0,8814
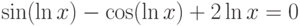
11	$\sin(\ln x)-\cos(\ln x)+2\ln x=0$	[1;3]	Половинного деления	1,3749
12	$x-2+\sin\frac{1}{x}=0$	[1,2;2]	Итераций	1,3077
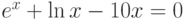
13	$e^x+\ln x-10x=0$	[3;4]	Ньютона	3,5265
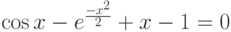
14	$\cos x-e^{\frac{-x^2}{2}}+x-1=0$	[1;2]	Половинного деления	1,0804
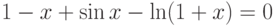
15	$1-x+\sin x-\ln(1+x)=0$	[0;1,5]	Итераций	1,1474
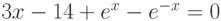
16	$3x-14+e^x-e^{-x}=0$	[1;3]	Ньютона	2,0692
17	$\sqrt{1-x}-\tg x=0$	[0;1]	Половинного деления	0,5768
18	$x+\cos(x^{0.52}+2)=0$	[0,5;1]	Итераций	0,9892
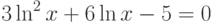
19	$3\ln^2 x+6\ln x-5=0$	[1;3]	Ньютона	1,8832
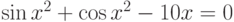
20	$\sin x^2+\cos x^2-10x=0$	[0;1]	Половинного деления	0,1010
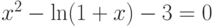
21	$x^2-\ln(1+x)-3=0$	[2;3]	Итераций	2,0267
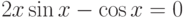
22	$2x\sin x-\cos x=0$	[0,4;1]	Ньютона	0,6533
23	$e^x+\sqrt{1+e^{2x}}-2=0$	[-1;0]	Половинного деления	-0,2877
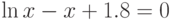
24	$\ln x-x+1.8=0$	[2;3]	Итераций	2,8459
25	$\sqrt[3]{x-4}-\frac{1}{x^2+1}=0$	[4;6]	Ньютона	4,0002
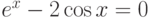
26	$e^x-2\cos x=0$	[0;2]	Половинного деления	0,5398
27	$\sqrt[3]{x+2}-3x+16=0$	[4;7]	Итераций	6,0000
28	$\frac{\pi\sin x}{x}-3\cos x-2=0$	[1;2]	Ньютона	1,5708