НОУ ИНТУИТ | Структуры и алгоритмы компьютерной обработки данных. Лекция 48: Задания

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 02.02.2011 | Доступ: свободный | Студентов: 3381 / 990 | Оценка: 4.43 / 3.57 | Длительность: 33:06:00

Тема: Программирование

Специальности: Программист

|

Вам нравится? Нравится 47 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

13. Бросание кубика. Кубик, грани которого помечены цифрами от 1 до 6, бросают раз. Найти вероятность того, что сумма выпавших чисел будет равна .

Ограничения: $1 \leq N \leq 500, 1 \leq Q \leq 3000$ , время 1 с.

Ввод из файла die.in. В первой строке находятся числа и через пробел.

Вывод в файл die.out. Выводится единственное вещественное число, которое должно отличаться от истинного значения не более чем на 0,01 истинного значения.

Примеры

14. Ближайшее число. Дана матрица размером $N\times N$ , заполненная неотрицательными целыми числами. Расстояние между двумя элементами $A_{ij}$ и $A_{pq}$ определено как |i – p| + |j – q| . Требуется заменить каждый нулевой элемент матрицы ближайшим ненулевым. Если есть две или больше ближайших ненулевых ячейки, нуль должен быть оставлен.

Ограничения: $1 \leq N \leq 200, 0 \leq A_{ij} \leq 1 000 000$ , время 3 с.

Ввод из файла neamum.in. В первой строке содержится число . Затем идут строк по чисел, разделенных пробелами и представляющих собой матрицу.

Вывод в файл neamum.out. Выводится строк по чисел, разделенных пробелами, – модифицированная матрица.

Пример

15. Прямоугольное деление. Дано прямоугольников со сторонами, параллельными осям координат. Требуется определить, на сколько частей эти прямоугольники разбивают плоскость (внутри частей не должно быть границ прямоугольников).

Ввод из файла rectpart.in. В первой строке содержится число прямоугольников . Далее идут строк, содержащих по четыре числа, x_1 y_1 x_2, y_2 , – координаты двух противоположных углов прямоугольника.

Ограничения: $1 \leq N \leq 100$ , координаты представляют собой целые числа и по абсолютной величине не превосходят 10 000, время 3 с.

Вывод в файл rectpart.out Вывести одно число – количество частей, на которые разбивается плоскость.

Пример

16. Водопровод. Город Восточный постоянно страдает от недостатка воды. Для устранения этой проблемы была построена новая водопроводная труба. Строительство трубы началось с обоих концов одновременно, и спустя некоторое время половины соединились. Ну, почти. Первая половина трубы заканчивалась в точке (х_1, у_1) , а вторая – в точке (x_2, у_2) . К сожалению, осталось лишь несколько отрезков трубы различной длины. Более того, из-за специфики местной технологии трубы могут быть проложены только в направлении с севера на юг или с востока на запад и соединяются, образуя или прямую, или угол 90 $\deg$ . Требуется, зная длины отрезков труб $L_1, L_2, \ldots, L_K$ и количество отрезков каждой длины $C_1, C_2, \ldots, C_K$ , сконструировать трубу, соединяющую две заданные точки, или определить, что это невозможно.

Ограничения: 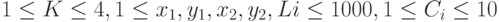$1 \leq K \leq 4, 1 \leq x_1, y_1, x_2, y_2, Li \leq 1000, 1 \leq C_i \leq 10$ , все числа целые, время 3 с.

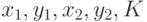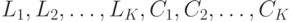Ввод из файла wpipe.in. В первой строке находятся числа x_1, y_1, x_2, y_2, K , затем чисел: $L_1, L_2, \ldots, L_K , C_1, C_2, \ldots, C_K$ .

Вывод в файл wpipe.out. Вывести одно число — минимальное количество нужных отрезков труб или -1, если соединение невозможно.

17. Химические реакции. Билл преподает химию в школе, он подготовил несколько тестов для учеников. Каждый тест состоит из химической формулы и нескольких возможных результатов реакции. Среди этих результатов ученики должны выбрать правильный. Билл хочет убедиться в том, что, вводя свои тесты в компьютер, он не допустил опечаток, благодаря которым ученики могли бы отбросить неверные ответы, просто подсчитав число химических элементов в левой и правой частях уравнения (в правильном уравнении химической реакции должно соблюдаться равенство).

Ваша задача - написать программу, которая поможет Биллу. Программа должна прочитать описание теста, состоящее из заданной левой части уравнения и нескольких возможных правых частей, и определить, равно ли количество химических элементов в каждой предложенной правой части уравнения количеству химических элементов в заданной левой части.

Билл формализовал задачу. И левая, и правая части уравнения представлены строкой символов без пробелов, состоящей из одной или более химических последовательностей, разделенных знаком плюс. Каждая последовательность имеет необязательный предшествующий целый множитель, относящийся ко всей последовательности, и несколько элементов. Каждый элемент может сопровождаться необязательным целым множителем, относящимся к нему. Элемент в этом уравнении может быть или отдельным химическим элементом, или целой последовательностью в круглых скобках. Каждый отдельный химический элемент представлен или одной прописной буквой, или прописной буквой, сопровождаемой строчной.

Еще более формально, используя нотацию, аналогичную форме Бэкуса-Наура, можно написать:

<формула>::=[<число>]<последовательность>{"+"[<число>]<последовательность>}
<последовательность>::=<элемент>[<число>]{<элемент>[<число>]} 
<элемент>::=<химический элемент>|"("<последовательность>")" 
<химический элемент>::=<прописная буква>[<строчная буква>] 
<прописная 6уква>::= "А".."Z" 
<строчная буква>::= "а".."z" 
<число>::= "1". ."9" {"0". ."9"}

Будем говорить, что каждый отдельный химический элемент встречается в формуле всего раз, если – сумма всех различных вхождений этого химического элемента, умноженных на все числа, относящиеся к ним. Например, в формуле

C2H5OH+3O2+3(SiO2)

C встречается всего 2 раза;
H встречается всего 6 раз (5 + 1);
0 встречается всего 13 раз (1 + 3 * 2 +3 * 2);
Si встречается всего 3 раза.

Все множители в формулах – целые числа не меньше 2, если заданы явно, или равны 1 – по умолчанию.

Ввод из файла chem.in. В первой строке находится формула — левая часть уравнения, во второй – одно число – количество рассматриваемых правых частей, в каждой из следующих строк – одна формула – предлагаемая правая часть уравнения.

Ограничения: $1 \leq N \leq 10$ , длина формулы не превосходит 100 символов, каждый

Вывод в файл chem.out. Для каждой из заданных правых частей выведите одну строку вида

<формула левой части>!=<формула правой части>

Здесь <формула левой части> должна быть замещена посимвольной копией формулы левой части, как она дана в первой строке входного файла, а <формула правой части> – замещена точной копией формулы правой части, как она дана во входном файле. В строках не должно быть пробелов.

Пример

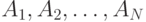18. Суммы. Дано целых чисел $A_1, A_2,\ldots, A_N$ . Требуется найти количество различных значений сумм вида k_1A_1 + k_2A_2 + k_NA_N .

Ограничения: 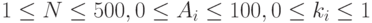$1 \leq N \leq 500, 0 \leq A_i \leq 100, 0 \leq k_i \leq 1$ , все числа целые, время 2 с.

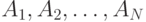Ввод из файла sums.in. В первой строке находится число , во второй – $A_1, A_2,\ldots, A_N$ .через пробел.

Вывод в файл sums.out. Вывести одно число – количество различных значений сумм.

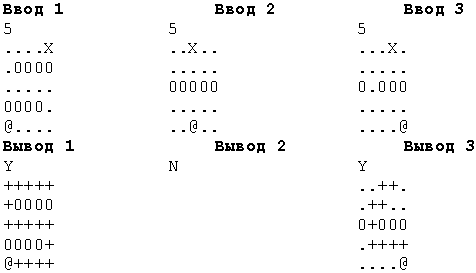
Примеры

19. Lines. В таблице из строк и столбцов некоторые клетки заняты шариками, другие свободны. Выбран шарик, который нужно переместить, и место, куда его нужно переместить. Выбранный шарик за один шаг перемещается в соседнюю по горизонтали или вертикали свободную клетку. Требуется выяснить, возможно ли переместить шарик из начальной клетки в заданную, и если возможно, то найти путь из наименьшего количества шагов.

Ограничения: 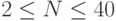$2 \leq N \leq 40$ , время 1 с.

Ввод из файла lihes.in. В первой строке находится число , в следующих строках – по символов. Символом точки обозначена свободная клетка, латинской заглавной – шарик, @ – исходное положение шарика, который должен двигаться, латинской заглавной — конечное положение шарика.

Вывод в файл lihes.out. В первой строке выводится , если движение возможно, или , если нет. Если движение возможно, далее следует строк по символов – как и на вводе, но буква , а также все точки по пути заменяются плюсами.

Примеры

20. Покраска лабиринта. Лабиринт представляет собой квадрат, состоящий из $N\times N$ сегментов. Каждый из сегментов может быть либо пустым, либо заполненным камнем. Гарантируется, что левый верхний и правый нижний сегменты пусты. Лабиринт обнесен сверху, снизу, слева и справа стенами, оставляющими свободными только левый верхний и правый нижний углы. Директор лабиринта решил покрасить стены лабиринта, видимые изнутри (рис.). Помогите ему рассчитать количество краски, необходимой для этого.

Ограничения: 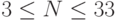$3 \leq N \leq 33$ , размер сегмента 3 x 3 м, высота стен 3 м, время 1 с.

Ввод из файла paintlab.in. В первой строке находится число , затем идут строк по символов: точка обозначает пустой сегмент, решетка – сегмент со стеной.

Вывод в файл paintlab.out. Вывести одно число – площадь видимой части внутренних стен лабиринта в квадратных метрах.

21. Поле для крикета. Жил-был жадный Король. Он приказал своему главному Архитектору построить поле для королевского крикета в парке. Король был таким жадным, что не послушал предложения своего Архитектора построить поле прямо в центре парка и окружить его живописным бордюром деревьев, специально посаженных вокруг. Вместо этого он приказал не срубать деревья и не сажать новых, но построить самое большое поле для крикета, какое только можно. Если Король обнаружит, что Архитектор посмел тронуть даже единственное дерево в парке или спроектировал меньшее поле, чем было возможно, Архитектор лишится головы. Более того, он потребовал от Архитектора представить план поля, где указаны его точное положение и размер.

Ваша задача – помочь бедному Архитектору сохранить голову, написав программу, которая найдет максимальный размер поля для крикета и его положение внутри парка, удовлетворяющие требованиям Короля.

Задача слегка упрощена тем, что парк Короля имеет прямоугольную форму и расположен на плоской поверхности. Более того, границы парка параллельны направлениям север – юг и восток – запад. В то же время игра в королевский крикет всегда происходит на квадратном поле, границы которого также параллельны направлениям север – юг и восток – запад. Архитектор уже сопоставил парку прямоугольную декартову систему координат и точно определил координаты каждого дерева.

Оси этой системы координат, конечно, параллельны направлениям север – юг и восток – запад. Юго-западный угол парка имеет координаты (0, 0), а северо-восточный – координаты 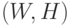(W, H) , где и – длина и ширина парка соответственно (рис.).

В этой задаче вы можете пренебречь диаметром деревьев. Деревья не могут находиться внутри поля для крикета, но могут располагаться на его сторонах. Поле для крикета может также касаться границы парка, но не должно лежать вне парка.

Ввод из файла cricket.in. Первая строка содержит три целых числа, , и , разделенных пробелами: — число деревьев в парке, и – длина и ширина парка соответственно.

Следующие строк описывают координаты деревьев в парке. Каждая строка содержит два целых числа x_i и y_i разделенных пробелом и представляющих собой координаты -го дерева. Все деревья имеют различные координаты.

Ограничения: $1 \leq N \leq 100, 1 \leq W, H \leq 10 000, 0 \leq x_i \leq W, 0 \leq y_i \leq H$ , время 1 с.

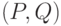Вывод в файл cricket.out. Вывести через пробел три целых числа, , и , где (P, Q) – координаты юго-западного угла поля для крикета, – длина его сторон. Если существует несколько возможных положений поля максимального размера, вывести любое.

Пример

22. Электронная таблица. Напишите программу, выполняющую функции очень простой электронной таблицы. Она работает с таблицей из 9 строк от 1 до 9 и 26 столбцов от А до Z. Клетки таблицы обозначаются именами, составленными из кодов столбца и строки, например B1, S8.

Каждая клетка содержит выражение. Выражения используют целые константы, ссылки на клетки, скобки, бинарные операторы +, -, * и / (целочисленное деление).

Так, 567, E8/2, (3+B3)*(C4-l) являются правильными выражениями. Все операторы целочисленные. Деление на ноль дает в результате ноль.

Если значение ячейки, на которую ссылается некоторое выражение, не определено, оно считается равным нулю. Ситуация, когда две или более ячейки зависят друг от друга, является отдельным случаем – циклической ссылкой.

Ограничения: длина выражения в одной ячейке до 255 символов, все аргументы и результаты меньше 1 000 000, время 1 с.

Ввод из файла sprsheet.in. Первая строка содержит число выражений . Следующие N строк имеют формат <Имя клетки>=<выражение>. Все выражения корректные, и каждая ячейка определена не более чем одним выражением.

Вывод в файл sprsheet.out. В единственной строке выводится или значение клетки A1, или число 1000000 (один миллион), если значение клетки A1 не может быть найдено из-за циклической ссылки.

Пример

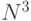23. Путь спелеолога. Пещера представлена кубом, разбитым на частей по каждому измерению (то есть на N^3 кубических клеток). Каждая клетка может быть или пустой, или полностью заполненной камнем. Исходя из положения спелеолога в пещере, требуется найти, какое минимальное количество перемещений по клеткам ему требуется, чтобы выбраться на поверхность. Переходить из клетки в клетку можно, только если они обе свободны и имеют общую грань.

Ограничения: 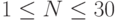$1 \leq N \leq 30$ , время 1 с.

Ввод из файла speleo.in. В первой строке содержится число . Далее следует блоков. Блок состоит из пустой строки и строк по символов: # обозначает клетку, заполненную камнями, точка – свободную клетку. Начальное положение спелеолога обозначено заглавной буквой . Первый блок представляет верхний уровень пещеры, достижение любой свободной его клетки означает выход на поверхность. Выход на поверхность всегда возможен.

Вывод в файл speleo.out. Вывести одно число – длину пути до поверхности.

Пример

Комментарий

Нужно спуститься на уровень вниз, сделать два движения на запад, подняться на уровень вверх, сделать движение на юг, подняться на уровень вверх.

24. Дырявая ткань. На столе лежат несколько кусков ткани, не перекрывая друг друга. Эти куски могут иметь дыры, в том числе и настолько большие, что в них может поместиться целый кусок ткани. Был получен черно-белый образ поверхности стола, на котором области, покрытые тканью, представлены символами *, а свободные площади – точками. Один кусок ткани, таким образом, представлен 4-связной областью символов *, то есть группой *, соседствующих друг с другом горизонтально или вертикально, но не по диагонали.

На схеме три куска – один без дыр, а два – с одной дырой каждый: первый – площадью 8, второй – площадью 12.

Ваша цель – найти кусок с наибольшим количеством дыр в нем. Дыра – это 4-связная область точек, полностью окруженных символами *. Если несколько кусков имеют одинаковое количество дыр, нужно выбрать кусок минимальной площади.

Ввод из файла holey.in. В первой строке содержатся два числа и , разделенные пробелами. Следующие строк содержат по символов каждая. Символы в этих строках – или * (ASCII 42), или точка (ASCII 46).

Ограничения: $1 \leq W, H \leq 100$ , время 1 с.

Вывод в файл holey.out. Вывести одно целое число – площадь минимального из наиболее дырявых кусков. Если нет кусков с дырами, выходной файл должен содержать ноль.

Пример

25. Несоставляемое число. Даны натуральных чисел. Найти минимальное натуральное число, не представимое суммой никаких из этих чисел, если в эту сумму каждое исходное число может входить не более одного раза.

Ограничения: $1 \leq N \leq 10 000$ , значения исходных чисел от 1 до 1 000 000 000, время 1 с.

Ввод из файла nosum.in. В первой строке находится число , в следующих строках – по одному натуральному числу.

Вывод в файл nosum.out. Вывести одно число.

Примеры

26. SMS. Сообщения SMS сотового телефона MOBILA (рис.) составлены из прописных латинских букв. Если буква первая на кнопке, нужно нажать эту кнопку один раз, чтобы добавить букву в сообщение. Если буква вторая — нужно нажать кнопку дважды и т. д. Так, чтобы набрать слово "SMS", нужно нажать

(PQRS)(PQRS)(PQRS)(PQRS)(MNO)(PQRS)(PQRS)(PQRS)(PQRS)

Чтобы ввести две буквы, находящиеся на одной кнопке, нужно между нажатиями клавиши сделать паузу. Например, чтобы ввести сообщение "АА", нужно нажать (АВС)(пауза)(АВС)

Если на кнопке три буквы, то, как только такая кнопка нажата три раза, последняя буква добавляется в сообщение немедленно, а следующие нажатия той же кнопки относятся к следующей букве сообщения. Аналогично, если на кнопке четыре буквы, то после четырех нажатий в сообщение будет добавлена последняя буква. То есть последовательность нажатий

(АВС)(АВС)(АВС)(АВС)(пауза)(АВС)

соответствует сообщению "САА". К сожалению, сотовые телефоны этой модели давно не производятся, и остался только один такой телефон. Он может произвольно вставлять и игнорировать паузы во время ввода сообщения, что может привести к некоторым изменениям в сообщениях. Например, введя MOSCOWQUARTERFINAL, можно получить вместо этого OMSCMNWQTTARTERPDEINAL. Вы получили SMS-сообщение и знаете, что оригинальное сообщение содержало букв.

Чтобы определить вероятность угадывания оригинального сообщения, найдите число возможных сообщений, которые могли превратиться в то, которое вы получили.

Ограничения: $1 \leq N \leq 80$ , полученное сообщение состоит только из прописных латинских букв, длина полученного сообщения – от 1 до 80 букв, время 2 с.

Ввод из файла sms.in. В первой строке задана длина оригинального сообщения . Вторая строка содержит полученное SMS-сообщение.

Вывод в файл sms.out. Вывести число сообщений из букв, которые, будучи набранными на этом телефоне, могут превратиться в данное сообщение.

Примеры

27. Lines. В таблице из строк и столбцов некоторые клетки заняты шариками, другие свободны. Выбран шарик, который нужно переместить, и место, куда его нужно переместить. Выбранный шарик за один шаг перемещается в соседнюю по горизонтали или вертикали свободную клетку. Требуется выяснить, возможно ли переместить шарик из начальной клетки в заданную, и если возможно, то найти путь из наименьшего количества шагов.

Ограничения: 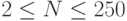$2 \leq N \leq 250$ , время 1 с.

Ввод из файла lines2.in. В первой строке находится число , в следующих строках – по символов. Символом точки обозначена свободная клетка, латинской заглавной 0 — шарик, @ — исходное положение шарика, который должен двигаться, латинской заглавной — конечное положение шарика.

Вывод в файл lines2.out. В первой строке выводится , если движение возможно, или , если нет. Если движение возможно, далее следует строк по символов – как и на вводе, но , а также все точки по пути заменяются плюсами.

Примеры

28. Удаление клеток. Из прямоугольного листа клетчатой бумаги ( строк, столбцов) удалили некоторые клетки. На сколько кусков распадется оставшаяся часть листа? Две клетки не распадаются, если они имеют общую сторону.

Ограничения: 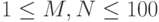$1 \leq M, N \leq 100$ , время 1 с.

Ввод из файла remsquar.in. В первой строке находятся числа и , в следующих строках – по символов. Если клетка не была вырезана, этому соответствует знак #, если вырезана – точка.

Вывод в файл remsquar.out. Вывести одно число.

Пример

Дальше >>

Авторизоваться

Структуры и алгоритмы компьютерной обработки данных

Задания

Вопросы и ответы