Задания
Задание 10. Алгоритмы обработки данных
1. Закраска прямой. На числовой прямой окрасили  отрезков. Известны координаты левого и правого концов каждого отрезка (
отрезков. Известны координаты левого и правого концов каждого отрезка ( 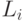 и
и 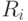 ). Найти длину окрашенной части числовой прямой.
). Найти длину окрашенной части числовой прямой.
Ограничения: 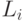 и
и 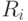 – целые,
– целые,  ,
,  , время 1 с.
, время 1 с.
Ввод из файла cover.in. В первой строке находится число  , в следующих
, в следующих  строках – пары
строках – пары 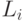 и
и 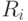 .
.
Вывод в файл cover.out. Вывести одно число – длину окрашенной части прямой.
Примеры
2. Сумма произведений. Дан набор переменных 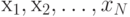 . Каждая переменная
. Каждая переменная 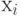 может принимать значение только -1, 0 или +1. Для данного целого числа
может принимать значение только -1, 0 или +1. Для данного целого числа  требуется определить количество способов присвоить переменным
требуется определить количество способов присвоить переменным 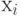 значения так, чтобы сумма всех возможных произведений
значения так, чтобы сумма всех возможных произведений  была равна
была равна  , где
, где  и
и 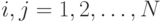 . Два способа считаются различными, если они содержат различное число
. Два способа считаются различными, если они содержат различное число  .
.
Ограничения:  ,
,  , время 1 с.
, время 1 с.
Ввод из файла prodsum.in. В первой строке находятся числа  и
и  , разделенные пробелом.
, разделенные пробелом.
Вывод в файл prodsum.out. Вывести одно целое число – количество способов представить  как сумму произведений.
как сумму произведений.
Примеры
3. Статическая сложность. Анализ временной сложности алгоритмов – важный инструмент создания эффективных программ. Алгоритмы, выполняемые за линейное время, как правило, значительно быстрее алгоритмов, требующих для выполнения той же задачи квадратичного времени, так что предпочтение должно быть отдано первым.
Обычно определяют время выполнения алгоритма по отношению к  – "размеру" входных данных. Это может быть число объектов, которые нужно отсортировать, число точек многоугольника и т.п. Поскольку определение формулы зависимости временной сложности алгоритма от
– "размеру" входных данных. Это может быть число объектов, которые нужно отсортировать, число точек многоугольника и т.п. Поскольку определение формулы зависимости временной сложности алгоритма от  – непростая задача, было бы замечательно, если бы ее можно было автоматизировать. К сожалению, в общем случае это невозможно. Но в этой задаче мы будем рассматривать программы очень простой природы, над которыми это можно проделать. Рассматриваемые программы записаны согласно следующим правилам БНФ, где <число> может быть любым неотрицательным целым числом:
– непростая задача, было бы замечательно, если бы ее можно было автоматизировать. К сожалению, в общем случае это невозможно. Но в этой задаче мы будем рассматривать программы очень простой природы, над которыми это можно проделать. Рассматриваемые программы записаны согласно следующим правилам БНФ, где <число> может быть любым неотрицательным целым числом:
<Программа> : := "BEGIN" <Список операторов> "END" <Список операторов>::=<Оператор>|<Оператор><Список операторов> <Оператор> ::=<Оператор LOOP> | <Оператор 0P> <Оператор LOOP> ::=<Заголовок ЮОР><Список операторов>"END" <Заголовок LOOP> : := "LOOP" <число> | "LOOP n" <Оператор OP> : := "OP" <число>
Время выполнения такой программы может быть вычислено следующим образом: выполнение оператора ОР требует столько единиц времени, сколько указано в его параметре. Список операторов, заключенный в оператор LOOP, выполняется столько раз, сколько указано в параметре оператора, то есть или заданное константное число раз, если задано число, или  раз, если параметром является
раз, если параметром является  . Время выполнения списка операторов равно сумме времени выполнения его частей. Таким образом, время выполнения программы в целом зависит от
. Время выполнения списка операторов равно сумме времени выполнения его частей. Таким образом, время выполнения программы в целом зависит от  .
.
Ввод из файла icomplex.in. В первой строке находится целое число  — число программ во входном файле. Затем идут
— число программ во входном файле. Затем идут  программ, удовлетворяющих приведенной грамматике. Пробелы и переводы строк могут встречаться везде в программе, но не в ключевых словах BEGIN, END, LOOP и OP, нет их и в целых числах.
программ, удовлетворяющих приведенной грамматике. Пробелы и переводы строк могут встречаться везде в программе, но не в ключевых словах BEGIN, END, LOOP и OP, нет их и в целых числах.
Вывод в файл icomplex.out Для каждой программы сначала идет строка с номером программы. В следующей строке записывается время работы программы в терминах  – многочлен степени не более 10. Многочлен должен быть записан обычным способом, то есть подобные слагаемые должны быть приведены, слагаемое большей степени должно предшествовать слагаемому меньшей степени, слагаемые с коэффициентом 0 не записываются, множители 1 не записываются. Общий вид второй строки " Runtime = a*n^10+b*n^9+...+i*n^2+j*n+k ". Если время выполнения нулевое, нужно вывести " Runtime = 0 ". За строкой с многочленом должна следовать пустая строка.
– многочлен степени не более 10. Многочлен должен быть записан обычным способом, то есть подобные слагаемые должны быть приведены, слагаемое большей степени должно предшествовать слагаемому меньшей степени, слагаемые с коэффициентом 0 не записываются, множители 1 не записываются. Общий вид второй строки " Runtime = a*n^10+b*n^9+...+i*n^2+j*n+k ". Если время выполнения нулевое, нужно вывести " Runtime = 0 ". За строкой с многочленом должна следовать пустая строка.
Ограничения: вложенность операторов LOOP не превышает 10, размер входного файла не более 2 Кбайт, коэффициенты многочлена в ответе не превышают 50 000, время 1 с.
Пример
4. Строки Фибоначчи. Строку Фибоначчи  для натуральных чисел
для натуральных чисел  определим так:
определим так:  при
при  , где "+" означает конкатенацию строк. Требуется найти количество вхождений строки
, где "+" означает конкатенацию строк. Требуется найти количество вхождений строки  , состоящей из символов
, состоящей из символов  и
и  , в строку Фибоначчи
, в строку Фибоначчи  .
.
Ограничения: Длина строки  составляет от 1 до 25 символов,
составляет от 1 до 25 символов,  , время 1 с.
, время 1 с.
Примечание. Длина  равна 1 134 903 170.
равна 1 134 903 170.
Ввод из файла fibostr.in. В первой строке содержится число  , во второй – строка
, во второй – строка  .
.
Вывод в файл fibostr.out. Вывести одно число – количество вхождений строки  в строку Фибоначчи
в строку Фибоначчи  .
.
Примеры
5. Анти-QuickSort. Для сортировки последовательности чисел широко используется быстрая сортировка – QuickSort. Оценивать время работы алгоритма будем количеством сравнений с элементами массива (то есть суммарным количеством сравнений в первом и втором while ). Требуется написать программу, генерирующую тест, на котором быстрая сортировка сделает наибольшее число таких сравнений.
Ввод из файла antiqs.in. В первой строке находится единственное число  .
.
Ограничения:  , время 1 с.
, время 1 с.
Вывод в файл antiqs.out. Вывести перестановку чисел от 1 до  , на которой быстрая сортировка выполнит максимальное число сравнений. Если таких перестановок несколько, вывести любую из них.
, на которой быстрая сортировка выполнит максимальное число сравнений. Если таких перестановок несколько, вывести любую из них.
Пример
6. Путь коня. Дана шахматная доска, состоящая из  клеток; несколько из них вырезано. Провести ходом коня через невырезанные клетки путь минимальной длины из одной заданной клетки в другую.
клеток; несколько из них вырезано. Провести ходом коня через невырезанные клетки путь минимальной длины из одной заданной клетки в другую.
Ограничения: 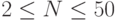 , время 1 с.
, время 1 с.
Ввод из файла knightw.in. В первой строке задано число  . В следующих
. В следующих  строках содержится по
строках содержится по  символов. Символом # обозначена вырезанная клетка, точкой – невырезанная клетка, @ — заданные клетки (таких символов два).
символов. Символом # обозначена вырезанная клетка, точкой – невырезанная клетка, @ — заданные клетки (таких символов два).
Вывод в файл knightw.out. Если путь построить невозможно, вывести "Impossible", в противном случае вывести такую же карту, как и на входе, но пометить все промежуточные положения коня символом @.
Примеры
7. Грядки. Прямоугольный садовый участок шириной  и длиной
и длиной  метров разбит на квадраты со стороной 1 м. На этом участке вскопаны грядки. Грядкой называется совокупность квадратов, удовлетворяющая таким условиям:
метров разбит на квадраты со стороной 1 м. На этом участке вскопаны грядки. Грядкой называется совокупность квадратов, удовлетворяющая таким условиям:
- из любого квадрата этой грядки можно попасть в любой другой квадрат этой же грядки, последовательно переходя по грядке из квадрата в квадрат через их общую сторону;
- никакие две грядки не пересекаются и не касаются друг друга ни по вертикальной, ни по горизонтальной сторонам квадратов (касание грядок углами квадратов допускается).
Подсчитайте количество грядок на садовом участке.
Ограничения:  , время 1 с.
, время 1 с.
Ввод из файла beds.in. В первой строке находятся числа  и
и  через пробел, далее идут
через пробел, далее идут  строк по
строк по  символов. Символ # обозначает территорию грядки, точка соответствует незанятой территории. Других символов в исходном файле нет.
символов. Символ # обозначает территорию грядки, точка соответствует незанятой территории. Других символов в исходном файле нет.
Вывод в файл beds.out. Вывести одно число – количество грядок на садовом участке.
Пример
8. Упорядоченные дроби. Вывести в порядке возрастания все несократимые дроби, заключенные между 0 и 1, знаменатели которых не превышают  .
.
Ограничения:  , время 1 с.
, время 1 с.
Ввод из файла ordfrac.in. В первой строке находится единственное число  .
.
Вывод в файл ordfrac.out. В каждой строке выводится дробь.
Пример
9. Сообщение. В сообщении, состоящем из одних русских букв и пробелов, каждую букву заменили ее порядковым номером в русском алфавите (А – 1, Б – 2, ... , Я – 33), а пробел – нулем. Требуется по заданной последовательности цифр найти количество исходных сообщений, из которых она могла получиться.
Ограничения: цифр не более 100, время 1 с.
Ввод из файла message.in. В первой строке содержится последовательность цифр.
Вывод в файл message.out. Вывести одно число.
Пример
10. Умножение многочленов. Ввести в символьной форме два многочлена от х с целыми коэффициентами и вывести их произведение в порядке убывания степеней – также в символьной форме.
Ограничения: степень исходных многочленов не более 10, коэффициенты исходных многочленов по модулю не более 104, время 1 с.
Ввод из файла polymul.in. В двух строках находятся многочлены.
Вывод в файл polymul.out. В единственной строке выводится многочлен.
Примеры
11. Гомер Симпсон. Обеденный перерыв Гомера Симпсона составляет  мс. Один гамбургер Гомер съедает за
мс. Один гамбургер Гомер съедает за  мс, один чизбургер — за
мс, один чизбургер — за  . Требуется найти максимальное суммарное число гамбургеров и чизбургеров, которые Гомер может съесть в течение обеденного перерыва.
. Требуется найти максимальное суммарное число гамбургеров и чизбургеров, которые Гомер может съесть в течение обеденного перерыва.
Ограничения: 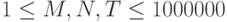 , все числа целые, время 2 с.
, все числа целые, время 2 с.
Ввод из файла homer.in. В первой строке находятся три числа –  ,
,  и
и  , разделенные пробелами.
, разделенные пробелами.
Вывод в файл homer.out. Вывести максимальное суммарное число гамбургеров и чизбургеров. Если остается какое-то время, требуется указать его через пробел. Предпочтителен вариант, когда дополнительного времени остается как можно меньше.
Примеры
12. Диалог компьютеров. Три компьютера соединены сетью. Один из них – сервер, два других – клиенты. На сервере есть несколько файлов. Полные имена файлов, состоящие из двух частей (имя и расширение), различны. Оба клиента знают полные имена всех файлов, находящихся на сервере. Сервер выбирает один из своих файлов и посылает его имя одному из клиентов, а расширение – второму.
Затем клиенты начинают общаться друг с другом, пытаясь определить, какой файл был выбран сервером (они хотят узнать полное имя файла). Однако клиенты вынуждены общаться очень ограниченным способом. Они по очереди посылают сообщения друг другу, но могут сказать только, что не знают полного имени файла. Если клиент не знает полного имени выбранного файла, он может послать другому клиенту сообщение, говорящее: "Я не знаю полного имени файла". Клиенты чередуются, посылая только это сообщение туда и обратно. Так продолжается до тех пор, пока один из клиентов не узнает полное имя файла или они не решат закончить диалог. Клиент, получивший первую часть полного имени файла, всегда ждет, что второй клиент пошлет первое сообщение.
Пусть вы знаете все полные имена файлов, находящихся на сервере, и слушаете разговор клиентов. Основываясь на этой беседе, вы должны определить набор файлов, которые могли быть выбраны сервером. Файлы в этом наборе называются файлами-кандидатами.
Ввод из файла dialogue.in. В первой строке находятся два целых числа,  и
и  , разделенные пробелом:
, разделенные пробелом:  – число файлов на сервере,
– число файлов на сервере,  – число сообщений, посланных клиентами, пытающимися определить полное имя файла.
– число сообщений, посланных клиентами, пытающимися определить полное имя файла.
Каждая из следующих  строк содержит одно полное имя файла. Полное имя файла дано в стиле, аналогичном формату 8.3 MS-DOS. Каждое полное имя представлено в форме имя.расширение, где и имя, и расширение состоят только из заглавных латинских букв и цифр. Имя всегда имеет от одного до восьми символов. Расширение имеет до трех символов и может быть пусто. Если расширение пусто, разделяющая точка может быть опущена.
строк содержит одно полное имя файла. Полное имя файла дано в стиле, аналогичном формату 8.3 MS-DOS. Каждое полное имя представлено в форме имя.расширение, где и имя, и расширение состоят только из заглавных латинских букв и цифр. Имя всегда имеет от одного до восьми символов. Расширение имеет до трех символов и может быть пусто. Если расширение пусто, разделяющая точка может быть опущена.
Каждое полное имя файла появляется во входном файле не более одного раза.
Ограничения:  , время 3 с.
, время 3 с.
Вывод в файл dialogue.out. В первой строке выводится число файлов-кандидатов для данных набора файлов и числа сообщений между клиентами. Выводится 0, если файлы-кандидаты отсутствуют.
В следующих строках находятся полные имена файлов-кандидатов, каждое в отдельной строке. Они должны идти в том же порядке и в том же написании, что и во входном файле. Это означает, что если разделяющая точка в названии конкретного файла была опущена во входном файле, то она должна быть опущена и в выводе, и наоборот. Файл нельзя упоминать более одного раза.
Пример












