Алгоритмы сортировки массивов. Внутренняя сортировка

Цель лекции: изучить основные алгоритмы внутренних сортировок и научиться решать задачи сортировок массивов различными методами (бинарная пирамидальная сортировка, метод Шелла, быстрая сортировка Хоара, сортировка слиянием).

Сортировка является одной из фундаментальных алгоритмических задач программирования. Решению проблем, связанных с сортировкой, посвящено множество научных исследований, разработано множество алгоритмов.

В общем случае сортировку следует понимать как процесс перегруппировки заданного множества объектов в определенном порядке. Сортировка применяется во всех без исключения областях программирования, будь то базы данных или математические программы.

Алгоритмом сортировки называется алгоритм для упорядочения некоторого множества элементов. Обычно под алгоритмом сортировки подразумевают алгоритм упорядочивания множества элементов по возрастанию или убыванию.

В случае наличия элементов с одинаковыми значениями, в упорядоченной последовательности они располагаются рядом друг за другом в любом порядке. Однако иногда бывает полезно сохранять первоначальный порядок элементов с одинаковыми значениями.

В алгоритмах сортировки лишь часть данных используется в качестве ключа сортировки. Ключом сортировки называется атрибут (или несколько атрибутов), по значению которого определяется порядок элементов. Таким образом, при написании алгоритмов сортировок массивов следует учесть, что ключ полностью или частично совпадает с данными.

Практически каждый алгоритм сортировки можно разбить на 3 части:

• сравнение, определяющее упорядоченность пары элементов;
• перестановку, меняющую местами пару элементов;
• собственно сортирующий алгоритм, который осуществляет сравнение и перестановку элементов до тех пор, пока все элементы множества не будут упорядочены.

Алгоритмы сортировки имеют большое практическое применение. Их можно встретить там, где речь идет об обработке и хранении больших объемов информации. Некоторые задачи обработки данных решаются проще, если данные заранее упорядочить.

Оценка алгоритмов сортировки

Ни одна другая проблема не породила такого количества разнообразнейших решений, как задача сортировки. Универсального, наилучшего алгоритма сортировки на данный момент не существует. Однако, имея приблизительные характеристики входных данных, можно подобрать метод, работающий оптимальным образом. Для этого необходимо знать параметры, по которым будет производиться оценка алгоритмов.

• Время сортировки – основной параметр, характеризующий быстродействие алгоритма.
• Память – один из параметров, который характеризуется тем, что ряд алгоритмов сортировки требуют выделения дополнительной памяти под временное хранение данных. При оценке используемой памяти не будет учитываться место, которое занимает исходный массив данных и независящие от входной последовательности затраты, например, на хранение кода программы.
• Устойчивость – это параметр, который отвечает за то, что сортировка не меняет взаимного расположения равных элементов.
• Естественность поведения – параметр, которой указывает на эффективность метода при обработке уже отсортированных, или частично отсортированных данных. Алгоритм ведет себя естественно, если учитывает эту характеристику входной последовательности и работает лучше.

Классификация алгоритмов сортировок

Все разнообразие и многообразие алгоритмов сортировок можно классифицировать по различным признакам, например, по устойчивости, по поведению, по использованию операций сравнения, по потребности в дополнительной памяти, по потребности в знаниях о структуре данных, выходящих за рамки операции сравнения, и другие.

Наиболее подробно рассмотрим классификацию алгоритмов сортировки по сфере применения. В данном случае основные типы упорядочивания делятся следующим образом.

• Внутренняя сортировка – это алгоритм сортировки, который в процессе упорядочивания данных использует только оперативную память (ОЗУ) компьютера. То есть оперативной памяти достаточно для помещения в нее сортируемого массива данных с произвольным доступом к любой ячейке и собственно для выполнения алгоритма. Внутренняя сортировка применяется во всех случаях, за исключением однопроходного считывания данных и однопроходной записи отсортированных данных. В зависимости от конкретного алгоритма и его реализации данные могут сортироваться в той же области памяти, либо использовать дополнительную оперативную память.
• Внешняя сортировка – это алгоритм сортировки, который при проведении упорядочивания данных использует внешнюю память, как правило, жесткие диски. Внешняя сортировка разработана для обработки больших списков данных, которые не помещаются в оперативную память. Обращение к различным носителям накладывает некоторые дополнительные ограничения на данный алгоритм: доступ к носителю осуществляется последовательным образом, то есть в каждый момент времени можно считать или записать только элемент, следующий за текущим; объем данных не позволяет им разместиться в ОЗУ.

Внутренняя сортировка является базовой для любого алгоритма внешней сортировки – отдельные части массива данных сортируются в оперативной памяти и с помощью специального алгоритма сцепляются в один массив, упорядоченный по ключу.

Следует отметить, что внутренняя сортировка значительно эффективней внешней, так как на обращение к оперативной памяти затрачивается намного меньше времени, чем к носителям.

Рассмотрим основные алгоритмы внутренних сортировок, которые называются усовершенствованными (логарифмическими).

Бинарная пирамидальная сортировка

Данный метод сортировки был предложен Дж. У. Дж. Уильямсом и Р.У. Флойдом в 1964 году. Пирамидальная сортировка в некотором роде является модификацией такого подхода, как сортировка выбором, с тем лишь отличием, что минимальный (или максимальный) элемент из неотсортированной последовательности выбирается за меньшее количество операций. Для такого быстрого выбора из этой неотсортированной последовательности строится некоторая структура. Именно суть данного метода и состоит в построении такой структуры, которая называется пирамидой.

Пирамида (сортирующее дерево, двоичная куча) – двоичное дерево с упорядоченными листьями (корень дерева – наименьший или наибольший элемент). Пирамиду можно представить в виде массива. Первый элемент пирамиды является наименьшим или наибольшим, что зависит от ключа сортировки.

Просеивание – это построение новой пирамиды по следующему алгоритму: новый элемент помещается в вершину дерева, далее он перемещается ("просеивается") по пути вниз на основе сравнения с дочерними элементами. Спуск завершается, если результат сравнения с дочерними элементами соответствует ключу сортировки.

Последовательность чисел x_i,x_i+1,...,x_n формирует пирамиду, если для всех k=i, i+1,...,n/2 выполняются неравенства x_k > x_2k, x_k > x_i (или x_k < x_2k, x_k < x_2k+1 ). Элементы x_2i и x_2i+1 называются потомками элемента x_i.

Массив чисел 12 10 7 5 8 7 3 является пирамидой. Такой массив удобно изображать в виде дерева. Первый элемент массива, элементы которого образуют собой пирамиду, является наибольшим (или наименьшим). Если массив представлен в виде пирамиды, то массив легко отсортировать.

Алгоритм пирамидальной сортировки.

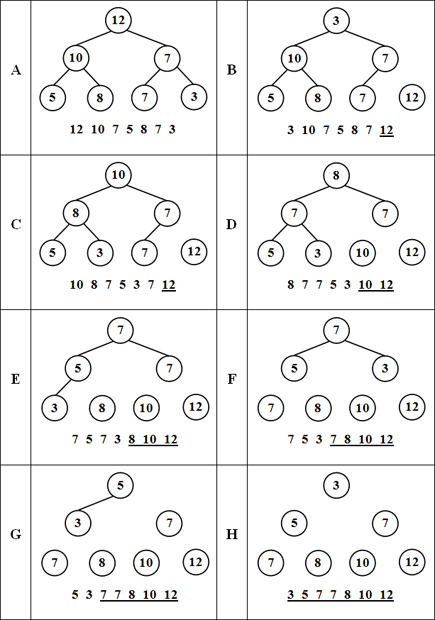
Шаг 1. Преобразовать массив в пирамиду (рис. 42.1. А).

Шаг 2. Использовать алгоритм сортировки пирамиды (рис. 42.1. В – H).

Алгоритм преобразования массива в пирамиду (построение пирамиды). Пусть дан массив x[1],x[2],...,x[n].

Шаг 1. Устанавливаем k=n/2.

Шаг 2. Перебираем элементы массива в цикле справа налево для i=k,k-1,...,1. Если неравенства x_i > x_2i, x_i > x_2i+1 не выполняются, то повторяем перестановки x_i с наибольшим из потомков. Перестановки завершаются при выполнении неравенств x_i > x_2i, x_i > x_2i+1.

Алгоритм сортировки пирамиды.

Рассмотрим массив размерности n, который представляет пирамиду x[1],x[2],...,x[n].

Шаг 1. Переставляем элементы x[1] и x[n].

Шаг 2. Определяем n=n-1. Это эквивалентно тому, что в массиве из дальнейшего рассмотрения исключается элемент x[n].

Шаг 3. Рассматриваем массив x[1],x[2],...,x[n-1], который получается из исходного за счет исключения последнего элемента. Данный массив из-за перестановки элементов уже не является пирамидой. Но такой массив легко преобразовать в пирамиду. Это достигается повторением перестановки значения элемента из x[1] с наибольшим из потомков. Такая перестановка продолжается до тех пор, пока элемент из x[1] не окажется на месте элемента x[i] и при этом будут выполняться неравенства x[i] > x[2i], x[i] > x[2i+1]. Тем самым определяется новое место для значения первого элемента из x[1] (рис. 42.1. С).

Шаг 4. Повторяем шаги 2, 3, 4 до тех пор, пока не получим n=1. Произвольный массив можно преобразовать в пирамиду (рис. 42.1. D – H).

увеличить изображение
Рис. 42.1. Демонстрация бинарной пирамидальной сортировки по неубыванию

Построение пирамиды, ее сортировка и "просеивание" элементов реализуются с помощью рекурсии. Базой рекурсии при этом выступает пирамида из одного элемента, а сортировка и просеивание элементов сводятся посредством декомпозиции к аналогичным действиям с пирамидой из n-1 элемента.

//Описание функции бинарной пирамидальной сортировки
void Binary_Pyramidal_Sort (int k,int *x){
  Build_Pyramid(k/2+1,k-1,x);
  Sort_Piramid(k-1,x);
}

//Построение пирамиды
void Build_Pyramid (int k, int r, int *x){
  Sifting(k,r,x);
  if (k > 0)
    Build_Pyramid(k-1,r,x);
}

//Сортировка пирамиды
void Sort_Piramid (int k, int *x){
  Exchange (0,k,x);
  Sifting(0,k-1,x);
  if (k > 1)
    Sort_Piramid(k-1,x);
}

//"Просеивание" элементов
void Sifting (int left, int right, int *x){
  int q, p, h;
  q=2*left+1;
  p=q+1;
  if (q <= right){
    if (p <= right && x[p] > x[q]) 
      q = p;
    if (x[left] < x[q]){
      Exchange (left, q, x);
      Sifting(q, right, x);
    }
  }
}
//процедура обмена двух элементов
void Exchange (int i, int j, int *x){
  int tmp;
  tmp = x[i];
  x[i] = x[j];
  x[j] = tmp;
}

Теоретическое время работы этого алгоритма можно оценить, учитывая, что пирамидальная сортировка аналогична построению пирамиды методом просеивания (при этом не учитывается начальное построение пирамиды). Поэтому время работы алгоритма пирамидальной сортировки без учета времени построения пирамиды будет определяться по формуле T₁(n)=O(nxlog n).

Построение пирамиды занимает T₂(n)=O(n) операций за счет того, что реальное время выполнения функции построения зависит от высоты уже созданной части пирамиды.

Тогда общее время сортировки (с учетом построения пирамиды) будет равно: T(n)=T₁(n)+T₂(n)=O(n)+O(nxlog n)=O(nxlog n).

Пирамидальная сортировка не использует дополнительной памяти. Метод не является устойчивым: по ходу работы массив так "перетряхивается", что исходный порядок элементов может измениться случайным образом. Поведение неестественно: частичная упорядоченность массива никак не учитывается. Данная сортировка на почти отсортированных массивах работает также долго, выигрыш ее получается только на больших n.