Рекурсивные функции

Цель лекции: изучить понятия рекурсии, рекурсивные функции в программировании, приемы построения рекурсивной триады при решении задач, научиться применять рекурсивные методы в решении задач на языке С++.

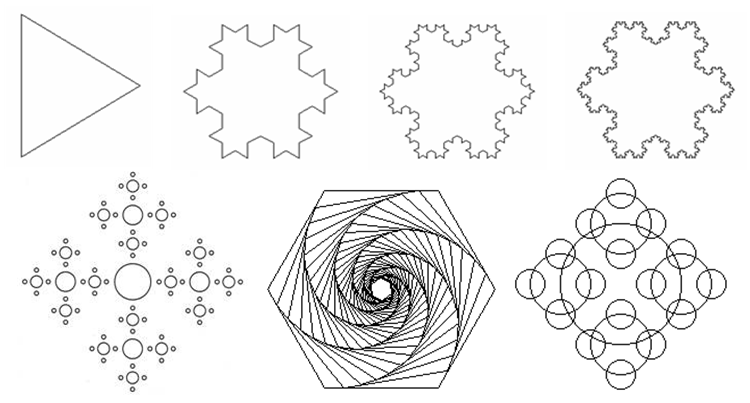
В окружающем нас мире часто можно встретить объекты, обладающие самоподобием. То есть часть большого объекта в чем-то сходна с самим объектом. Например, ветка дерева повторяет форму и характер ветвления, схожие с самим деревом. Приведенные ниже графические объекты также обладают самоподобием (рис. 3.1). Такие объекты называются рекурсивными.

Рис. 3.1. Рекурсивные графические объекты

При первичном осмыслении понятие рекурсии достаточно просто и не требует специальных знаний. Иногда на рекурсию смотрят как на наличие в определении объекта ссылки на сам объект или проявление свойств самоповторения (при этом сколь угодно малая часть объекта подобна всему объекту в целом). Общий случай проявления рекурсивности может быть сформулирован как наличие циклических взаимных обращений в определении объекта, которые в итоге замыкаются на сам объект.

В технике процедурного программирования рекурсивность в построении подпрограмм проявляется в разработке управляющих структур, которые при выполнении обращаются сами к себе непосредственно или через цепочку других аналогичных структур. Бесконечность и незавершенность таких обращений кажущаяся, так как при достижении определенных условий самовызовы завершаются. Во многих конкретных случаях простыми рассуждениями путем отслеживания значений одной или нескольких управляющих величин удается провести доказательство завершимости рекурсивных вычислений за конечное число шагов.

Рекурсивность в постановке задачи проявляется, если решение для общего случая сводится к аналогичным задачам для меньшего количества входных данных. В таком контексте под рекурсией понимают прием последовательного сведения решения некоторой задачи к решению совокупности "более простых" задач такого же класса и получению на этой основе решения исходной задачи.

Рекурсия в широком смысле – это определение объекта посредством ссылки на себя. Рекурсия в программировании – это пошаговое разбиение задачи на подзадачи, подобные исходной.

Рекурсивный алгоритм – это алгоритм, в определении которого содержится прямой или косвенный вызов этого же алгоритма.

В языках программирования процедурной парадигмы предусмотрено использование рекурсивных функций в решении задач.

Функция называется рекурсивной, если в своем теле она содержит обращение к самой себе с измененным набором параметров. При этом количество обращений конечно, так как в итоге решение сводится к базовому случаю, когда ответ очевиден.

Пример 1. В арифметической прогрессии найдите a_n, если известны а₁ = -2.5, d =0.4, не используя формулу n -го члена прогрессии.

По определению арифметической прогрессии, a_n=a_n-1+d, при этом

an-1=an-2+d, an-2=an-3+d,... a2=a1+d.

Таким образом, нахождение a_n для номера n сводится к решению аналогичной задачи, но только для номера n -1, что в свою очередь сводится к решению для номера n -2, и так далее, пока не будет достигнут номер 1 (значение а₁ дано по условию задачи).

float arifm (int n, float a, float d) {
  if (n<1) return 0;       // для неположительных номеров
  if (n==1) return a;      // базовый случай: n=1
  return arifm(n-1,a,d)+d; // общий случай
}

В рекурсивных функциях несколько раз используется return. В базовом случае возвращается конкретный результат (в примере – значение а ), а общий случай предусматривает вызов функцией себя же, но с меняющимися значениями отдельных параметров (в примере изменяется только номер члена последовательности, при этом не меняются разность и первый член прогрессии).

В программировании выделяют прямую и косвенную рекурсию. Прямая рекурсия предусматривает непосредственное обращение рекурсивной функции к себе, но с иным набором входных данных. Косвенная (взаимная) рекурсия представляет собой последовательность взаимных вызовов нескольких функций, организованная в виде циклического замыкания на тело первоначальной функции, но с иным набором параметров.

Для решения задач рекурсивными методами разрабатывают следующие этапы, образующие рекурсивную триаду:

• параметризация – выделяют параметры, которые используются для описания условия задачи, а затем в решении;
• база рекурсии – определяют тривиальный случай, при котором решение очевидно, то есть не требуется обращение функции к себе;
• декомпозиция – выражают общий случай через более простые подзадачи с измененными параметрами.

Целесообразность применения рекурсии в программировании обусловлена спецификой задач, в постановке которых явно или опосредовано указывается на возможность сведения задачи к подзадачам, аналогичным самой задаче. При этом эффективность рекурсивного или итерационного способов решения одной и той же задачи определяется в ходе анализа работоспособности программы на различных наборах данных. Таким образом, рекурсия не является универсальным способом в программировании. Ее следует рассматривать как альтернативный вариант при разработке алгоритмов решения задач.

Повысить эффективность рекурсивных алгоритмов часто представляется возможным за счет пересмотра этапов триады. Например, введение дополнительных параметров, не оговоренных в условии задачи, в реализации декомпозиции могут быть применены другие соотношения, а также можно организовать расширение базовых случаев с сохранением промежуточных результатов.

Область памяти, предназначенная для хранения всех промежуточных значений локальных переменных при каждом следующем рекурсивном обращении, образует рекурсивный стек. Для каждого текущего обращения формируется локальный слой данных стека (при этом совпадающие идентификаторы разных слоев стека независимы друг от друга и не отождествляются). Завершение вычислений происходит посредством восстановления значений данных каждого слоя в порядке, обратном рекурсивным обращениям. В силу подобной организации количество рекурсивных обращений ограничено размером области памяти, выделяемой под программный код. При заполнении всей предоставленной области памяти попытка вызова следующего рекурсивного обращения приводит к ошибке переполнения стека.

Пример 2. Для целого неотрицательного числа n найдите его факториал.

Разработаем рекурсивную триаду.

Параметризация: n – неотрицательное целое число.

База рекурсии: для n =0 факториал равен 1.

Декомпозиция: n!=(n-1)!xn.

long factor (int n) {
  if (n<0) return 0;        // для отрицательных чисел
  if (n==0) return 1;       // базовый случай: n=0
  return factor(n-1)*n;     // общий случай (декомпозиция)
}

Рассмотрим задачи, для которых можно предложить рекурсивные алгоритмы решения, в то время как итерационные алгоритмы были бы сложными и искусственными.

Пример 3. Задача о коэффициентах Безу

Для любых натуральных чисел n и m найдите коэффициенты Безу, то есть такие целые a и b, что выполняется равенство: nod(n,m)=axn+bxm (где nod(n,m) – наибольший общий делитель n и m ).

Параметризация.

m, n – данные натуральные числа, неизменяемые параметры;

d – наибольший общий делитель данных чисел, неизменяемый параметр;

bm, bn – коэффициенты Безу при n и m соответственно, эти параметры меняются при очередном рекурсивном вызове функции.

База рекурсии. Если при очередном обращении к функции с передаваемыми параметрами выполняется равенство d=mxbm–nxbn, то коэффициенты Безу найдены. Требуется вывести линейную комбинацию.

Декомпозиция. Если равенство не выполняется, то инкрементно увеличиваем коэффициент при меньшем из чисел ( n или m ). Следующий вызов рекурсивной функции выполняется с измененным набором отдельных параметров. При этом снова проверяется база рекурсии, и рекурсивный алгоритм повторяется (либо достигается база и функция завершает работу, либо выполняется декомпозиционный переход).

//Коэффициенты Безу
#include "stdafx.h"
#include <iostream>
using namespace std;
int nod(int m, int n);
void bezu(int d, int m, int n, int bm, int bn);

int _tmain(int argc, _TCHAR* argv[]){
  int x,y,del,buf;
  printf("Задача нахождения коэффициентов Безу");
  printf("\nВведите два натуральных числа:"); 
  printf("\nX= "); 
  scanf("%d",&x);
  printf("Y= "); 
  scanf("%d",&y);
  if (x < y) {buf = x; x = y; y = buf;} 
  del=nod(x,y);
  printf("\nЛинейная комбинация:\n");
  bezu(del,x,y,1,1);
  system("pause");
  return 0;
}

//функция нахождения наибольшего общего делителя двух чисел
int nod(int m, int n){
  if (m%n==0) return n;
  return nod(n,m%n);
}
//функция нахождения и вывода на экран коэффициентов Безу
void bezu(int d, int m, int n, int bm, int bn){ 
  int pm,pn;
  pm = m * bm;
  pn = n * bn;
  //проверка базы рекурсии (выполнение линейной комбинации)
  if (d == pm - pn) 
    printf ("%d = %d*%d - %d*%d", d, bm, m, bn, n);
  //декомпозиция
  else {
    bn++;
    pn=n*bn;
    /*если произведение pm больше, чем pn, то порядок 
    параметров сохраняется*/
    if (pm > pn) bezu(d, m, n, bm, bn);
    /*если произведение pm меньше, чем pn, то порядок 
    параметров изменятеся*/
    else  bezu(d, n, m, bn, bm); 
  }
}