Алгоритмы на графах. Алгоритмы обхода графа
Цель лекции: изучить основные алгоритмы обхода графа и научиться решать задачи обхода графа на основе поиска в ширину и поиска в глубину.
Теория графов в последнее время широко используется в различных отраслях науки и техники. Быстрое развитие данная теория получила с созданием электронно-вычислительной техники, которая позволяла решить многие задачи алгоритмизации.
Граф – это совокупность двух конечных множеств: множества точек и множества линий, попарно соединяющих некоторые из этих точек. Множество точек называется вершинами (узлами) графа. Множество линий, соединяющих вершины графа, называются ребрами (дугами) графа.
Ориентированный граф (орграф) – граф, у которого все ребра ориентированы, т.е. ребрам которого присвоено направление.
Неориентированный граф (неорграф) – граф, у которого все ребра неориентированы, т.е. ребрам которого не задано направление.
Смешанный граф – граф, содержащий как ориентированные, так и неориентированные ребра.
Петлей называется ребро, соединяющее вершину саму с собой. Две вершины называются смежными, если существует соединяющее их ребро. Ребра, соединяющие одну и ту же пару вершин, называются кратными.
Простой граф – это граф, в котором нет ни петель, ни кратных ребер.
Мультиграф – это граф, у которого любые две вершины соединены более чем одним ребром.
Маршрутом в графе называется конечная чередующаяся последовательность смежных вершин и ребер, соединяющих эти вершины.
Маршрут называется открытым, если его начальная и конечная вершины различны, в противном случае он называется замкнутым.
Маршрут называется цепью, если все его ребра различны. Открытая цепь называется путем, если все ее вершины различны.
Замкнутая цепь называется циклом, если различны все ее вершины, за исключением концевых.
Граф называется связным, если для любой пары вершин существует соединяющий их путь.
Вес вершины – число (действительное, целое или рациональное), поставленное в соответствие данной вершине (интерпретируется как стоимость, пропускная способность и т. д.). Вес (длина) ребра – число или несколько чисел, которые интерпретируются по отношению к ребру как длина, пропускная способность и т. д.
Взвешенный граф – граф, каждому ребру которого поставлено в соответствие некое значение (вес ребра).
Выбор структуры данных для хранения графа в памяти компьютера имеет принципиальное значение при разработке эффективных алгоритмов. Рассмотрим несколько способов представления графа.
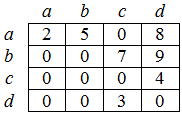
Пусть задан граф (например, рис. 44.1), у которого количество вершин равно n, а количество ребер – m. Каждое ребро и каждая вершина имеют вес – целое положительное число. Если граф не является помеченным, то считается, что вес равен единице.
- Список ребер – это множество, образованное парами смежных вершин ( рис. 44.2). Для его хранения обычно используют одномерный массив размером m, содержащий список пар вершин, смежных с одним ребром графа. Список ребер более удобен для реализации различных алгоритмов на графах по сравнению с другими способами.
- Матрица смежности – это двумерный массив размерности n x n, значения элементов которого характеризуются смежностью вершин графа ( рис. 44.3). При этом значению элемента матрицы присваивается количество ребер, которые соединяют соответствующие вершины. Данный способ действенен, когда надо проверять смежность или находить вес ребра по двум заданным вершинам.
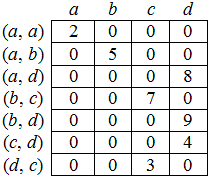
- Матрица инцидентности – это двумерный массив размерности n x m, в котором указываются связи между инцидентными элементами графа (ребро и вершина). Столбцы матрицы соответствуют ребрам, строки – вершинам ( рис. 44.4). Ненулевое значение в ячейке матрицы указывает связь между вершиной и ребром. Данный способ является самым емким для хранения, но облегчает нахождение циклов в графе.
Существует много алгоритмов на графах, в основе которых лежит систематический перебор вершин графа, такой что каждая вершина просматривается (посещается) в точности один раз. Поэтому важной задачей является нахождение хороших методов поиска в графе.
Под обходом графов (поиском на графах) понимается процесс систематического просмотра всех ребер или вершин графа с целью отыскания ребер или вершин, удовлетворяющих некоторому условию.
При решении многих задач, использующих графы, необходимы эффективные методы регулярного обхода вершин и ребер графов. К стандартным и наиболее распространенным методам относятся:
Эти методы чаще всего рассматриваются на ориентированных графах, но они применимы и для неориентированных, ребра которых считаются двунаправленными. Алгоритмы обхода в глубину и в ширину лежат в основе решения различных задач обработки графов, например, построения остовного леса, проверки связности, ацикличности, вычисления расстояний между вершинами и других.