Модели нейронов
Элементы нейронных сетей и задача разделения двух классов
Персептрон
Простой персептрон — это нейрон МакКаллока-Питса (рис.1). Весовые
коэффициенты входов сумматора, на которые подаются входные сигналы 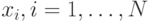 обозначаются
обозначаются 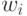 , а пороговое значение —
, а пороговое значение —  . Нелинейная функция активации
. Нелинейная функция активации  персептрона является ступенчатой, вследствие чего выходной сигнал нейрона
может
принимать только два значения — 0 и 1 в соответствии с правилом
персептрона является ступенчатой, вследствие чего выходной сигнал нейрона
может
принимать только два значения — 0 и 1 в соответствии с правилом
 |
( 1) |
или -1 и 1 в соответствии с правилом
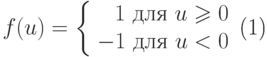 |
( 2) |
где  обозначает выходной сигнал сумматора
обозначает выходной сигнал сумматора
 |
( 3) |
В формуле (3) предполагается  .
.
Обучение персептрона состоит в
таком подборе весов 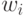 ,
чтобы выходной сигнал
,
чтобы выходной сигнал 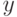 совпадал с заданным значением
совпадал с заданным значением 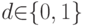 или
или 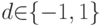 .
.
С персептроном связана задача четкого разделения двух классов по
обучающей выборке, которая ставится следующим образом: имеется два набора
векторов 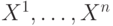 и
и 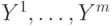 . Заранее
известно, что
. Заранее
известно, что 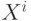 ,
, 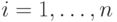 относятся к первому классу, а
относятся к первому классу, а 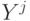 ,
,  - ко второму.
Требуется построить решающее правило, т.е. определить такую функцию
- ко второму.
Требуется построить решающее правило, т.е. определить такую функцию  , что при
, что при 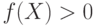 вектор
вектор  относится
к первому классу, а при
относится
к первому классу, а при 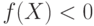 - ко второму.
- ко второму.

